Гелий Салахутдинов - Блеск и нищета К. Э. Циолковского

"Формула К.Э. Циолковского, опубликованная в 1903 году, получена для произвольного закона изменения массы (подчеркнуто А.К.)", - отметил А.А. Космодемьянский [27, с. 85], а поэтому и приоритет принадлежит К.Э. Циолковскому.

При этом была допущена небольшая, но существенная историческая неточность: автор работы [27] представил дело таким образом, будто исходное уравнение было записано К.Э. Циолковским в таком виде:

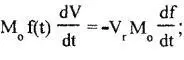
где f(t) - функция, определяющая закон изменения массы. У К.Э. Циолковского она, дескать, f(0) = l, а линейный и показательный законы изменения массы, принятые англичанами, являются, частным случаем f(t).

Однако, во-первых, К.Э. Циолковский f(t) не вводил, не оговаривал и вообще не знал ничего о законах изменения массы. Это впервые и в конкретной форме сделали цитировавшиеся англичане. Во-вторых, случай f(0) = l - всего лишь начальное условие.

Наконец, скорость ракеты в конце активного участка для рассматриваемого случая вообще не зависит от закона изменения массы. Поэтому выражения для формулы скорости у англичан и у К.Э. Циолковского тождественны, а вот вычисление расстояний требует введения этого закона, что он в отличии от англичан не понял вообще.

Вместе с тем, как бы ни закончился спор о его приоритете с англичанами, приоритет в решении уравнения тела с переменной массой ему не принадлежит в любом случае.

В России это уравнение впервые было решено другим нашим соотечественником, крупнейшем специалистом по теоретической механике, специализировавшемся именно на исследованиях движения тел переменной массы, бывшим приват-доцентом Санкт-Петербургского университета, а с 1902 года - ординарным профессором кафедры теоретической механики Петербургского политехнического института Мещерским Иваном Всеволодовичем (1859 - 1935 гг.). 27 марта 1897 года он представил свою диссертацию с решением этого уравнения в деканат, в ноябре того же года она уже была опубликована, а 10 декабря состоялась защита. По данным [172, с. 146] свое уравнение К.Э. Циолковский решил в мае 1897 года, а опубликовал, как уже отмечалось, только в 1903 году.

Сам А.А. Космодемьянский в предисловии к работе [36] писал: "Диссертация Мещерского "Динамика точки переменной массы" и его работа "Уравнения движения точки переменной массы в общем случае" составляют надежный теоретический фундамент современной ракетодинамики". И далее: "И.В. Мещерский - создатель нового раздела теоретической механики" [36, с. 25]. "Механикател переменной массы есть научная основа современной ракетодинамики" [36, с. 5].

Полученные И.В. Мещерским уравнения используются во всех видах летательных аппаратов, где происходит отделение (ракеты) или присоединение (воздушно-реактивные двигатели) массы.

Во второй главе он решает простейший случай этого уравнения, когда "скорость изменяющейся массы равна скорости точки" [36, с. 41].

Сейчас, при решении вопроса о приоритете К.Э. Циолковского, многие исследователи отмечают, что он свою формулу получил применительно к движению ракет, а И.В. Мещерский, якобы, лишь для некоторого абстрактного случая.

Однако даже беглое ознакомление с его работами [36] убедительно свидетельствуют, что и это утверждение несостоятельное.

И.В. Мещерский писал:

"Глава III содержит задачи о прямолинейном движении точки переменной массы и, прежде всего, те, к которым мы приходим, рассматривая вертикальное движение горящей ракеты и привязного аэростата ... и далее решается задача о движении тяжелой точки массы m = m 0(1 + at) 2при сопротивлении среды, пропорциональном квадрату скорости" [36, с. 43]. Решение этой задачи он свел к известному уравнению Риккати. В главе VI он рассматривал движение точки переменной массы в однородном поле тяготения, в том числе и когда масса точки изменяется по показательному закону [36, с. 122]. Основное уравнение ракеты (формула К.Э. Циолковского) было представлено в виде [36, с. 121]: X = а ln(f) + Х 0, где f - безразмерная масса, а = const.

Иногда можно слышать суждения и о том, что К.Э. Циолковскому хотя и не принадлежит приоритет в решении рассматриваемого уравнения, но он был первым, кто применил известную формулу к расчетам межпланетной ракеты (а не просто ракеты). Однако, если следовать этой логике, необходимо было бы законам, скажем, Ньютона или таблице умножения присваивать имена тех исследователей, которые впервые применяли их в новых областях науки и техники. Использование известной формулы в другой области познания не является предметом приоритета.

Не удалось К.Э. Циолковскому с помощью простых расчетов по этой формуле получить и какие-либо серьезные выводы. Наоборот, эти расчеты были способом ввести читателей в заблуждение относительно принципиальной осуществимости космической ракеты. С их помощью он, как уже отмечалось "прятал" проблемы, стоявшие на пути в космос.

К.Э. Циолковский в одной из своих работ писал:

"Я многое открыл, что было уже открыто ранее меня. Значение таких работ я признаю только для самого себя, так как они давали мне уверенность в моих силах. Также должны смотреть на свои открытия ученые, сделавшие их после меня. Обвинять в заимствованиях, конечно, без доказательств нельзя. Все же я думаю, что как мои запоздалые работы, так и других ученых отчасти навеяны отголосками ранее опубликованных трудов. Молва и печать их распространяют иногда и без указания источников. Печатная дата - вот, что решает спор о первенстве (приоритете) и значении ученого" [116, л. 1].

Ну что ж, настало время вернуть свой долг И.В. Мещерскому или англичанам. Следует вспомнить еще одну горестную судьбу уравнения, впервые полученного и исследованного И.В. Мещерским в 1897 году. Оно являлось частным случаем уравнения (1) и, только спустя 31 год(!), итальянский математик Леви-Чивита еще раз его вывел и оно получило его имя: "уравнение Леви-Чивита" [36, с. 16]. И здесь следовало бы восстановить историческую справедливость - для этого, в частности, и существуют историки науки и техники, - и вернуть И.В. Мещерскому его уравнение.

Итак, мы не нашли у К.Э. Циолковского ни одной задачи, типичной для ракетодинамики, специфику которой он не понимал и подменял в результате сущность ракетного движения представлениями о движении абстрактного тела.

Вот, например, как он решал вторую свою задачу, хотя непонятно кто и когда присвоил ей его имя. Формулируется она так: "Пусть ракета движется поступательно по вертикали вверх в однородном поле силы тяжести и начальная скорость центра масс ракеты равна Vo. Требуется определить закон изменения скорости и расстояния (высоты) ракеты в зависимости от времени при различных законах изменения массы и найти максимальную высоту подъема ракеты" [29, с. 204].