Дмитрий Менделеев - Познание России. Заветные мысли (сборник)

Во-первых, n есть число не беспредельно большое, а ограниченное некоторым пределом N, показывающим тот средний наибольший возраст, примерно около 100 лет, до которого доживают люди в настоящее время и при котором их число впадает в пределы точности опытных чисел и выводимой формулы 8. Следовательно, при n = N величина у может быть принята равной нулю. В то же время должно признать прямо, судя по числам и действительности, что у, или число жителей, достигает при возрасте N своей наименьшей величины, а потому на основании известного закона минимумов В + 2 Сn при этом равно 0, т. е. В = — 2 CN. Во-вторых, выражая у в процентах, очевидно, что сумма всех у от 0 до N = 100, что разрешает отношение между С и N и приводит к следующему выводу, касающемуся А, В и С в формуле (I), а именно 9:

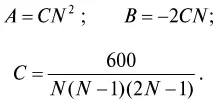
Подставляя эти выражения для А, В и С в уравнение (I), получим:

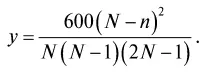
Это показывает, что по первому приближению, или первой законности в распределении числа жителей по возрастам, значение у -ов исчерпывается знанием n-ов и одним постоянным предельным возрастом N, а через это нахождение всей зависимости между у и n упрощается до крайности, т. е. из каждого отдельного значения и соответствующего ему n получается свое N. Если N расчесть на основании данных для малых возрастов, то выходит N не менее 110, даже до 115 лет. Если же это сделать на основании чисел уже стариков, то N выходит не только гораздо меньшим, но даже меньшим 100 лет, показывая этим, что в последние десятилетия вместе с возрастанием прироста (с отсутствием войн, развитием просвещения и пр.) увеличились условия для продолжительности человеческой жизни.

Это определяется, по всей вероятности, не столько успехом медицины и гигиены, сколько развитием благосостояния и уменьшением шансов погибнуть в зрелом возрасте, не доживая до старости; получаемые для разных значений n величины предельного возраста N, очевидно, не могут быть тождественны между собою и тем ближе к истине или вероятнейшему, чем более величина у. На основании этого и рассчитана средняя величина N, и она оказалась лежащею вблизи от N= 105 до N = 110 лет для той совокупности данных, которые взяты из приведенных выше переписей Германии и Соединенных Штатов. Подставляя эти числа, получаем

у = 0,000×2629(105 — n ) 2;

у = 0,000×2285(110 — n ) 2. (III)

Числа, рассчитанные по этим выражениям, приведены в последних столбцах табл. 2. Необходимость привести два ряда разочтенных чисел отчасти еще выясняется из последующего изложения.

Сличение разочтенных чисел с наблюдением для у -ов показывает, что наши выражения (I) или (II) вообще, а в частности (III) для Германии и Штатов недалеко отступают от действительности, т. е. что распределение населения по возрастам довольно точно выражается параболою 2-го порядка, т. е. в таком деле, как распределение по возрастам, господствует в норме при данных условиях правильная общая закономерность, что и требовалось показать для того, чтобы понемногу вселять убеждения в правильной закономерности социальных отношений, кажущихся капризными и сбивчивыми. Для показания этого же общего начала я приведу еще одно доказательство, относящееся к общему числу жителей С.-А. С. Штатов, но предварительно считаю не лишним остановиться над некоторыми обстоятельствами, относящимися к возрастному распределению.

Напомню, однако, вновь о том, что я не считаю свою формулу окончательною, а потому делаю лишь намеки на то, чего можно достичь со временем, когда найдется истинная формула и когда можно будет выводить из нее совершенно строгие следствия. Те следствия, которые выводятся из принятой нами формулы, очевидно суть только приблизительные, но и они наводят на такие размышления, которые, кажется, не следует упускать социологам из вида. Притом следствий этих много, а я могу здесь остановиться лишь над немногими из них, касающимися рождаемости, смертности, средней продолжительности жизни и среднего возраста всех жителей разных стран. Надо повторить при этом, что, признавая выставляемую закономерность лишь дающею первое приближение к истине, нельзя ручаться за полную точность выводимых следствий, но тем не менее над ними следует остановиться для того, собственно, что очень часто, особенно за последний век, числами, так сказать, баловались, не заботясь о приложении полученных выводов к каким бы то ни было жизненным явлениям, а моей заветною мыслью служит то соображение, что математический разбор явлений действительности тогда только служит для надлежащего уяснения предмета и для истинного познания вещей, когда он не только выводится из действительных данных, но когда в то же время он и дает следствия, непосредственно с действительностью связанные и представляющие для нее свой интерес.

Рождаемость, выраженная в процентных числах жителей, весьма сильно изменяется по странам, т. е. гораздо значительнее, чем распределение по возрастам. Для России она близка к 4,8 %, а во Франции — к 2,5 %; для других же стран Европы получаются промежуточные числа. Из формул можно полагать или ждать, что при N = 105 рождаемость ( n = 0) выражается 102,77 %, а при N = 110 она рассчитывается равною 2,76 %.

Для Германии рождаемость достигает ныне 3,7 %, если считать и мертворожденных, а за их исключением все же более 2,7–2,8 %, а именно около 3,5 %. Мне кажется, однако, что причину разности расчета от действительности должно приписывать не столько неполной точности нашей формулы, сколько тому, что в первое время после рождения и в Германии, как повсюду, мало умеют ухаживать за детьми и часть рожденных можно как бы причислить к мертворожденным, т. е. не считать в общем счете жителей. Но так как я считаю свои формулы (I) и (II) лишь первым приближением, и рождаемость представляет своего рода экстраполирование (т. е. расчет за пределом исходных данных, которые у нас начинаются с n = 1), то и не считаю надобным более останавливаться над этим предметом особенно потому, что в некоторых странах (Бельгия, Швейцария, Ирландия) распределение по возрастам близко отвечает нашему расчету (по III формуле) и в них рождаемость близка к 2,7 %, т. е. к формульной.

Мне кажется даже, что совпадение для некоторых стран (Бельгия, Швеция и др.) рождаемости с выводом, получаемым из распределения по возрастам, показывает, что в этих странах умеют столь же хорошо ухаживать за беременными матерями и новорожденными, как за лицами других возрастов.