Анатолий Фоменко - Введение в новую хронологию. Какой сейчас век?

Оказывается, важной характеристикой графика объема являются годы, в которые график делает ВСПЛЕСК, то есть достигает ЛОКАЛЬНОГО МАКСИМУМА. Эти всплески, то есть локальные максимумы указывают «подробно описанные годы» на отрезке времени (А,В) . В разных летописях «подробно описанными» могут оказаться, вообще говоря, разные годы.

Пусть С(t) — объем всех текстов, написанных о годе t современниками этого года. График С(t) сегодня НЕИЗВЕСТЕН, так как древние тексты утрачиваются со временем, информация исчезает.

Сформулируем МОДЕЛЬ ПОТЕРИ ИНФОРМАЦИИ:

ОТ ТЕХ ЛЕТ, В КОТОРЫЕ ИХ СОВРЕМЕННИКАМИ БЫЛО НАПИСАНО ОСОБЕННО МНОГО ТЕКСТОВ, — БОЛЬШЕ И ОСТАНЕТСЯ.

Другими словами, если фиксировать какой-то момент времени М справа от точки на рис. 3.2, то можем построить график СМ(Т) , показывающий объем текстов, которые «дожили» до момента времени М и описывают события года Т .

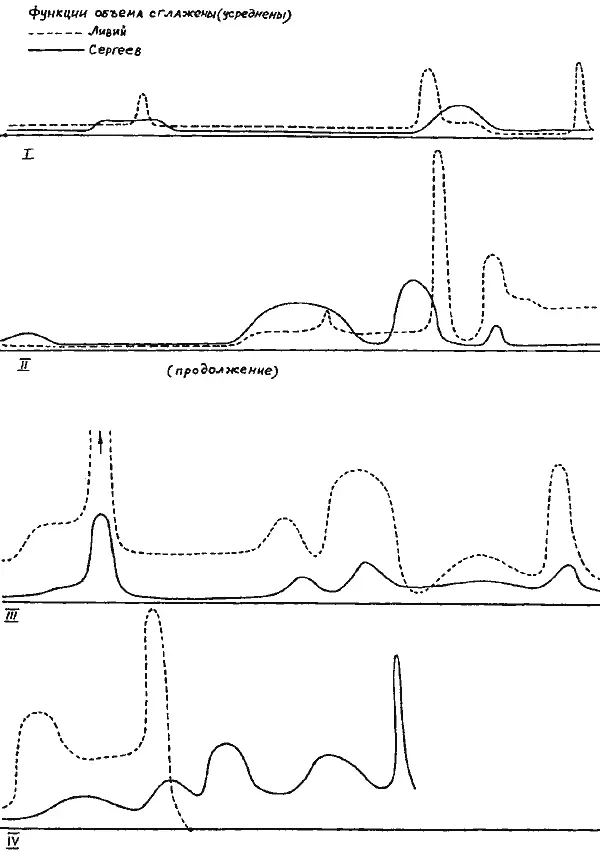
Рис. 3.2. Функции объема летописи «античного» Тита Ливия и современного учебника Сергеева. Налицо ярко выраженная корреляция

Другими словами, график СМ(Т) — это остаточный, сохранившийся фонд информации от эпохи (А, В) , который дошел до года М .

Наша модель может быть переформулирована, следовательно, таким образом:

ГРАФИК СМ(Т) ДОЛЖЕН ИМЕТЬ ВСПЛЕСКИ ПРИМЕРНО В ТЕ ЖЕ ГОДЫ НА ИНТЕРВАЛЕ (А,В) , ЧТО И ИСХОДНЫЙ ГРАФИК С(Т) .

Разумеется, проверить модель в таком ее виде трудно, поскольку график С(Т) первоначального фонда информации сегодня точно неизвестен. Но одно из следствий проверить можно.

Поскольку более поздние летописцы Х и Y , описывая один и тот же исторический период (А,В) , уже не являются современниками этих древних событий, то они вынуждены опираться на приблизительно один и тот же набор дошедших до них текстов. Следовательно, они должны «в среднем» более подробно описать именно те годы, от которых сохранилось больше текстов, и менее подробно — годы, о которых сохранилось мало информации. Другими словами, летописцы должны увеличивать подробность изложения при описании тех лет, от которых до них дошло больше текстов.

На языке графиков объема эта модель выглядит так. Если летописец X живет в эпоху М , то он будет опираться на фонд СМ(Т) . Если летописец Y живет в эпоху N , отличную, вообще говоря, от эпохи М , то он опирается на сохранившийся фонд CN(T) .

Естественно ожидать, что «в среднем» хронисты работают более или менее добросовестно, а потому они должны более подробно описать те годы из эпохи (А,В) , от которых до них дошло больше информации, текстов.

Другими словами, график объемов vol X(Т) будет иметь всплески примерно в те годы, где имеет всплески график СМ(Т) . В свою очередь, график vol Y(Т) будет иметь всплески примерно в те годы, где делает всплески график СN(Т) .

Но точки всплесков графика СМ(Т) близки к точкам всплесков исходного графика С(Т) . Аналогично, и точки всплесков графика СN(Т) близки к точкам всплесков графика С(Т) . Следовательно, графики vol X(T) и vol Y(Т) должны делать всплески ПРИМЕРНО ОДНОВРЕМЕННО, т. е. точки их локальных максимумов должны коррелировать. См. рис. 3.1.

При этом, конечно, амплитуды графиков могут быть существенно различны. Окончательно ПРИНЦИП КОРРЕЛЯЦИИ МАКСИМУМОВ формулируется так.

Графики объема «глав» для ЗАВИСИМЫХ летописей X и Y , т. е. для описывающих один и тот же исторический период (А,В) и одно и то же государство Г , ДОЛЖНЫ ОДНОВРЕМЕННО ДОСТИГАТЬ ЛОКАЛЬНЫХ МАКСИМУМОВ (ДЕЛАТЬ ВСПЛЕСКИ) на отрезке (А,В) , т. е. годы, «подробно описанные в X », и годы, «подробно описанные в Y » , должны быть близки или совпадать.

Напротив, если летописи X и Y НЕЗАВИСИМЫ, т. е. описывают либо разные исторические периоды (А,В) и (С,D) (одинаковой длины), либо разные государства, то графики объема для X и Y достигают локальных максимумов В РАЗНЫХ ТОЧКАХ. При этом считается, что для сравнения графиков следует совместить отрезки (А,В) и (С, D) .

Этот принцип подтвердится, если для большинства пар реальных, достаточно больших зависимых летописей Х и Y , т. е. описывающих одни и те же события, графики объема для X и Y делают всплески приблизительно одновременно, в одни и те же годы. При этом величина этих всплесков может быть существенно различной. Для реальных независимых хроник какая-либо корреляция точек всплесков должна отсутствовать. Конечно, для конкретных зависимых хроник одновременность всплесков графиков объема может иметь место лишь приблизительно.

Для количественной оценки близости точек всплесков поступим так. Вычислим число f(X,Y) — сумму квадратов чисел f[k] , где f[k] — расстояние в годах от точки всплеска с номером « k » графика объема X до точки всплеска с номером « k » графика объема Y . Если оба графика делают всплески одновременно, то моменты всплесков с одинаковыми номерами совпадают, и все числа f[k] равны нулю. Рассмотрев достаточно большой фиксированный запас различных реальных текстов H и, вычисляя для каждого из них число f(Х,Н) , отберем затем только такие тексты H , для которых это число не превосходит числа f(X,Y) . Подсчитав долю таких текстов во всем запасе текстов H , получаем коэффициент, который можно интерпретировать как вероятность р(Х,Y) . Более подробно описание р(Х,Y) см. в [416], [438], [419], [375]. Если коэффициент р(Х,Y) мал, то летописи X и Y зависимы. Если же коэффициент велик, то летописи X и Y независимы, т. е. сообщают о разных событиях.

В 1978–1980 гг. А.Т. Фоменко был проведен первый обширный вычислительный эксперимент по подсчету чисел р(Х,Y) для нескольких сотен пар конкретных исторических текстов — хроник, летописей и т. п. Детали см. в [416], [438], [419], [375].