Дмитрий Менделеев - Заветные мысли

Но и указанные отступления от нормы не должны, по существу, превосходить некоторого, притом небольшого, предела; например, не должны касаться целых процентов, а ограничиваться их долями, потому что числа извлечены из целого числа миллионов, а отступления касаются только сотен тысяч. Сколько мне известно, еще никто не принимался за вопрос о нормальном законе распределения числа жителей по возрастам, и если я решаюсь приняться за такой трудный новый опрос, то лишь по той причине, что верю в закон больших средних чисел и в правильность всяких отношений, кажущихся на первый взгляд зависящими лишь от частной воли и от случайного сцепления обстоятельств. Эта уверенность внушена долгим изучением явлений природы, а оно приводит к заключению, что все крупное общее среднее всегда оказывается закономерным, хотя всегда состоит из ряда мелочей, носящих на первый взгляд капризный индивидуальный характер.

Максвелловская теория газов – лучший пример для этого, и я не упущу случая внушить молодежи склонность к изучению представлений, подобных максвелловским, если хотят разобраться в вопросах социологии. Не желая усложнять изложения, я ограничиваюсь этим намеком и обращаюсь к примеру распределения народонаселения по возрастам как к такому, в котором можно уже видеть значение общих крупных чисел и закономерную в них стройность. Ведь механику, физику, химию изучали вначале исключительно приемами качественными и описательными, причем были, в сущности, рабами действительной природы, а понемногу становятся ее господами, подмечая присущую явлениям этого рода закономерность. Ведь и там изучению подлежат лишь частности, и всякое измерение сопряжено с неизбежными погрешностями, а общее крупное оказывается состоящим из данного числа капризных мельчайших отдельностей, в крупном же общем среднем все эти мелкие капризы исчезают, и тогда выступает основной, Божеский закон, который один делает рабов действительными господами предпринимаемого и предстоящего.

Не только в переносном, но и в подлинном смысле отдельный человек есть не что иное, как атом, и в совокупности людей, т. е. в крупных числах, до них относящихся, должно ждать такой же простоты и правильности, как в числах, получаемых от так называемой мертвой природы. Вот одна из тех заветных моих мыслей, которую очень желательно мне внушить будущим поколениям русского юношества, приложение которой к действительности я желал бы демонстрировать при помощи данных о народонаселении, и прежде всего о распределении по возрастам. Беглый взгляд на графическое выражение зависимости между у и n показывает уже, что они расположены по стройной, или, как привыкли выражаться математически, правильной, кривой линии. Найти законность – значит найти алгебраическую зависимость между у и n , т. е. между возрастом и числом жителей этого возраста. Геометрические соображения простейшего свойства показывают, что первое приближение к истине получится уже тогда, когда эту зависимость представим в виде вертикальной параболы, т. е. выразим:

у = А + Вn + Сn 2 (I)

где А, В и С – суть постоянные числа, а y и n – переменные (ординаты и абсциссы кривой). Ни одной минуты я не думаю, что такое выражение есть окончательное и вполне точное, утверждаю только, что оно очень близко удовлетворяет действительности и отступает от нее лишь на величины недалекие, подобные разностям между у 1-й и 2-й таблиц. Числа, разочтенные по формуле, приведены в последних столбцах табл. 2. Сходство вычисленных и наблюденных у наглядно показывает степень применимости вышеозначенной формулы.

Для ее нахождения, т. е. для определения числовых значений коэффициентов А, В, С, очевидно, достаточно трех данных, а их гораздо более. Каждые три данные у и n дадут свои коэффициенты, нужно найти некоторые вероятнейшие А, В и С и можно было бы руководствоваться при этом правилами способа наименьших квадратов, а так как n равно отстоят друг от друга, то можно было бы прибегнуть к известному приему моего покойного друга П. Л. Чебышева, развитому мною при исследовании колебания весов. Но в данном случае есть два соображения, упрощающих дело.

Во-первых, n есть число не беспредельно большое, а ограниченное некоторым пределом N, показывающим тот средний наибольший возраст, примерно около 100 лет, до которого доживают люди в настоящее время и при котором их число впадает в пределы точности опытных чисел и выводимой формулы 8. Следовательно, при n = N величина у может быть принята равной нулю. В то же время должно признать прямо, судя по числам и действительности, что у, или число жителей, достигает при возрасте N своей наименьшей величины, а потому на основании известного закона минимумов В + 2 Сn при этом равно 0, т. е. В = – 2 CN. Во-вторых, выражая у в процентах, очевидно, что сумма всех у от 0 до N = 100, что разрешает отношение между С и N и приводит к следующему выводу, касающемуся А, В и С в формуле (I), а именно 9:

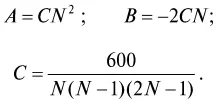
Подставляя эти выражения для А, В и С в уравнение (I), получим:

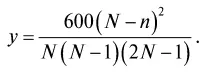
Это показывает, что по первому приближению, или первой законности в распределении числа жителей по возрастам, значение у -ов исчерпывается знанием n-ов и одним постоянным предельным возрастом N, а через это нахождение всей зависимости между у и n упрощается до крайности, т. е. из каждого отдельного значения и соответствующего ему n получается свое N. Если N расчесть на основании данных для малых возрастов, то выходит N не менее 110, даже до 115 лет. Если же это сделать на основании чисел уже стариков, то N выходит не только гораздо меньшим, но даже меньшим 100 лет, показывая этим, что в последние десятилетия вместе с возрастанием прироста (с отсутствием войн, развитием просвещения и пр.) увеличились условия для продолжительности человеческой жизни.

Это определяется, по всей вероятности, не столько успехом медицины и гигиены, сколько развитием благосостояния и уменьшением шансов погибнуть в зрелом возрасте, не доживая до старости; получаемые для разных значений n величины предельного возраста N, очевидно, не могут быть тождественны между собою и тем ближе к истине или вероятнейшему, чем более величина у. На основании этого и рассчитана средняя величина N, и она оказалась лежащею вблизи от N= 105 до N = 110 лет для той совокупности данных, которые взяты из приведенных выше переписей Германии и Соединенных Штатов. Подставляя эти числа, получаем