Игорь Дмитриев - Упрямый Галилей

Обратимся теперь еще к одному документу 1618 года – дневниковой записи Декарта, где он вкратце излагает свое решение задачи, предложенной Бекманом. Запись сделана вскоре после написания рассмотренного выше документа (возможно, что этот документ уже был отослан Бекману и дневниковую запись Декарт делал по памяти). Вот как он истолковал в дневнике вопрос Бекмана и свой ответ на него:

Камень, как он (то есть Бекман. – И.Д .) сказал, падает из точки A в точку B в течение часа [рис. 3.4]. Камень при этом постоянно притягивается Землей с одной и той же силой, не теряя скорости, запечатленной в нем предыдущим притяжением. По его [Бекмана] мнению, то, что движется в вакууме, будет двигаться всегда. Его вопрос: за какое время камень пройдет этот путь (то есть AD . – И.Д .)?

Как видим, в дневниковой записи вопрос Бекмана представлен в несколько иной формулировке, чем в первоначальном документе. Это неудивительно, поскольку задача Декартом уже была решена, и потому он переформулировал вопрос в более общем виде. Но – и это самое главное – Декарт в дневнике дает на поставленный вопрос (неважно, какой именно, ибо как бы вопрос ни формулировался, речь фактически шла о зависимости пути от времени при равноускоренном движении) совершенно иной ответ:

Я решил эту задачу. Площадь прямоугольного равностороннего треугольника [ ABC ] представляет собой движение. […Путь] AD будет пройден за время, представляемое [треугольником] ADE ; а [путь] DB – за время, представляемое [трапецией] DEBC . Следует также отметить, что меньшая площадь [фигуры] представляет более медленное движение. [Площадь] AED составляет одну треть [площади] DEBC (Декарт полагал, что AD = DB . – И.Д .). Поэтому он [камень] пройдет [путь] AD в три раза медленнее, чем [путь] DB 1484.

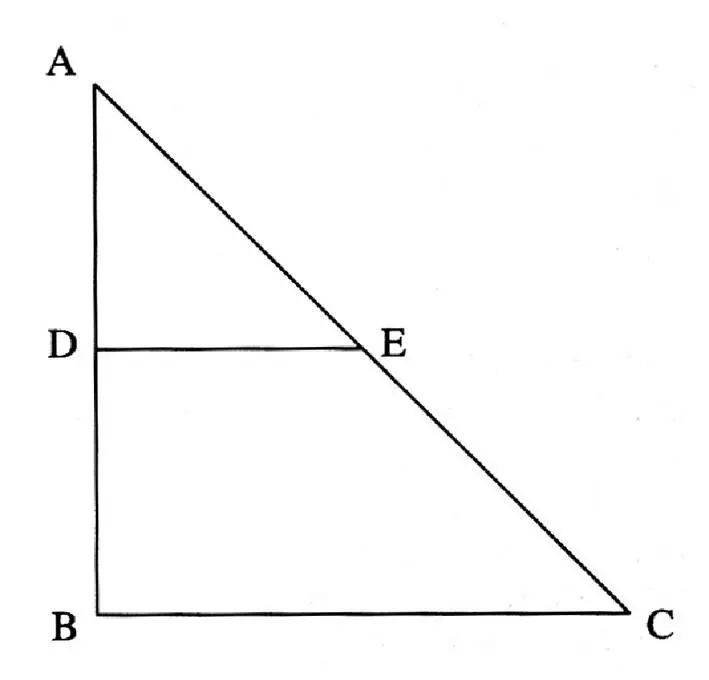
Рис. 3.4. К дневниковой записи Декарта по поводу задачи Бекмана (1618)

Нельзя сказать, что приведенная запись отличается ясностью формулировок (и это неудивительно, ведь Декарт делал ее для себя), но вместе с тем она вполне поддается трактовке и, на мой взгляд, совершенно однозначной. Запись эта означает, что расстояние AD камень пройдет со скоростью в три раза меньшей, чем расстояние DB . Если понимать выражение «пройти некий путь с некой скоростью V » в том смысле, что в конечной точке пути равноускоренно движущееся тело достигнет скорости V , то слова Декарта надо интерпретировать следующим образом: в точке D скорость камня будет в три раза меньше, чем в точке B , что, разумеется, неверно. (В действительности при условии AD = DB имеет место отношение V D/ V B= 1/√–2.) Если же приведенное выражение трактовать как время, требующееся для преодоления данного расстояния (полагая, что чем больше телу требуется времени для преодоления одного и того же расстояния, тем меньше его скорость, то есть V 1/ V 2= T 2/ T 1при S 1= S 2), то и тогда ответ Декарта неверен, ибо в действительности T AD/ T DB= (√–2/(2 – √–2)) при том же условии AD = DB .

Декарт же исходил из того, что «широта», то есть отрезок AB на рис. 3.4, представляет собой не время, как на рис. 3.2, но пройденный путь, тогда как площади фигур (треугольников и трапеций) на обоих рисунках представляют количество движения, накопленного телом к моменту прохождения им соответствующей части пути. Далее Декарт рассуждал так: площади фигур ADE и DEBC относятся как 1: 3. Следовательно, скорость, накопленная телом при прохождении отрезка DB , в три раза больше, чем скорость, накопленная при прохождении им равного по величине отрезка AD , то есть V D/ V B= (площадь треугольника ADB ): (площадь трапеции DEBC ) = 1: 3, а значит T AD/ T DB= 3: 1, так как V D/ V B= T DB/ T ADпри S 1= AD = DB = S 2. Иными словами, вторую половину пути камень прошел в три раза быстрее первой. Видимо, Декарт полагал, что результат не изменится оттого, что вместо времени вертикальный отрезок станет представлять пройденный путь.

Сказанное выше свидетельствует о том, что в 1618 году у Декарта не было «ясного и отчетливого», как он любил выражаться, понимания природы равноускоренного движения и понятия скорости.

Следующее из дошедших до нас упоминаний Декартом задачи о свободном падении тел относится к 1629 году. Весной и летом этого года указанная задача обсуждалась в переписке Бекмана с Мареном Мерсенном [рис. 3.5]. Последний спустя некоторое время попросил Декарта высказать свои соображения по теме полемики. Декарт затронул проблему свободного падения в двух письмах Мерсенну – от 13 ноября и от 18 декабря 1629 года 1485. Фактически Декарт повторил в них свои рассуждения, зафиксированные им в упомянутой дневникой записи 1618 года:

…Скорость движения в вакууме всегда возрастает в пропорции, о которой я упомянул выше и которую я нашел одиннадцать лет тому назад, когда передо мной была поставлена эта задача, и тогда же я записал решение в моем дневнике» 1486.

Рис. 3.5. Филипп де Шампань (Ph. de Champaigne; 1602 – 1674). Портрет Марена Мерсенна

Здесь я позволю себе небольшое отступление. В тоне Декартова письма нетрудно уловить приоритетные обертоны. Это не случайно. Осенью 1629 года Мерсенн получил от Декарта некоторые вопросы и соображения, касавшиеся природы консонанса в музыке, и переслал их Бекману. Последний в ответном письме сообщил Мерсенну, что эти вопросы он (Бекман) впервые поставил перед Декартом еще во время их встреч в Бреде. Узнав (из письма Мерсенна) об этом заявлении своего друга, Декарт решил, что тот хочет представить себя его (Декарта) наставником в 1618 – 1619 годах. Мысль о том, что Бекман мог его чему-то научить, привела самолюбивого Декарта в негодование, и он на время прекратил с голландцем всякие отношения. Спустя год Мерсенн, будучи в гостях у Бекмана, с интересом ознакомился с его «рукописной книгой» (то есть с Journal ), и последний не преминул вновь затронуть приоритетные вопросы. Узнав об этом, Декарт написал бывшему другу язвительное письмо, в котором заявил, что не слышал от него «ничего, кроме пустых фантазий», хотя, надо признать, «иногда случается, что, когда философские вопросы обсуждает даже совершенно не сведущий в них человек, он высказывает немало вещей, которые по чистой случайности совпадают с истиной» 1487.

Неужели только… как бы это помягче сказать… аристократическая гордость помешала Декарту признать, что кто-то мог его учить? Разумеется, это обстоятельство сыграло свою роль, ибо «основатель философского и научного рационализма» (Н. Грот) скорее был склонен учить других, чем следовать чьим-либо наставлениям 1488. Но была еще одна веская для Декарта причина столь негативно высказаться по поводу действительных или мнимых претензий Бекмана на интеллектуальное лидерство в их бредском тандеме. Декарт знал, что голландец собирается опубликовать свой трактат по физике, который должен был включать фрагменты из Journal . Если бы этот замысел оказался реализованным, то Декарту, который также планировал в конце 1620-х годов написать и издать пространное сочинение по физике, было бы очень трудно доказывать, какие идеи принадлежат ему, а какие Бекману. Французский мыслитель был не в восторге от того, что предлагавшиеся им объяснения природных явлений окажутся следствиями не интуитивно ясных первоначал мира, им же и сформулированных, но умозаключений некоего преподавателя из Дордрехта. Лучше уж быть обязанным Богу, конечному источнику наших интуитивно ясных понятий, нежели Бекману. Разумеется, воспрепятствовать публикации книги последнего 1489Декарт не мог, но он был в состоянии оказать психологическое давление на друга-соперника, возомнившего себя его учителем.