Дмитрий Усенков - Готовые дидактические материалы для тренировки устного счета: теорема Виета. 600 примеров

Теорема Виета, сформулированная французским математиком Франсуа Виетом, дает возможность в отдельных случаях (для целых и, иногда, для дробных значений корней) быстро находить решения квадратных уравнений, не прибегая к вычислениям с использованием дискриминанта. В школьной алгебре теорема Виета (формула Виета) играет такую же ведущую роль, как и теорема Пифагора в геометрии, однако учебно-методических материалов для отработки навыков поиска корней по формуле Виета имеется крайне мало.

Данное пособие призвано хотя бы частично устранить этот дефицит и содержит 600 готовых примеров квадратных уравнений с целыми корнями, а также ответы на эти примеры для проверки и самоконтроля.

При использовании в классно-урочной форме работы учитель может использовать текст пособия в качестве готового раздаточного материала, а после выполнения работы учащимися произвести проверку по имеющимся готовым ответам.

При использовании пособия для самостоятельной подготовки вы можете использовать ответы для самопроверки после решения выбранных примеров.

Ответы записаны в форме разложения квадратного уравнения на множители; если требуется получить значения самих корней, то нужно константные слагаемые в скобках брать с противоположными знаками.

Примечание.При использовании формулы Виета дискриминант квадратного уравнения должен быть неотрицательным. В случае, если дискриминант равен нулю, считается, что данное уравнение имеет два равных друг другу корня.

Формулировка теоремы Виета:

Сумма корней x 2+ bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Таким образом, если уравнение x 2+ bx + c = 0 имеет два корня: x 1и x 2, то справедливы следующие два равенства:

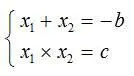
Согласно этим равенствам, для получения решения квадратного уравнения необходимо подбором найти два числа, сумма которых равна коэффициенту при x , взятому с обратным знаком, а произведение равно свободному члену. Следует заметить, что при этом исходное квадратное уравнение должно быть приведено к виду, когда коэффициент a при x 2равен единице.

Докажем теорему Виета.

Формулы для вычисления корней квадратного уравнения (рассматривается ситуация, когда дискриминант D положителен; уравнение с нулевым дискриминантом можно считать частным случаем):

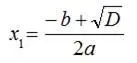
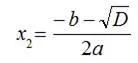
Вычислим сумму этих корней:

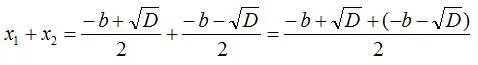
Раскрыв скобки и сократив слагаемые, получаем:

.

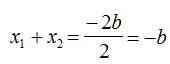
Вычислим произведение корней:

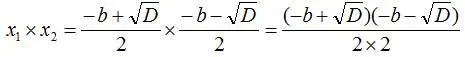
Применив в числителе формулу разности квадратов, получаем:

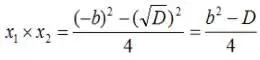
Подставляем известную нам формулу для вычисления дискриминанта:

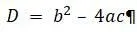
Получаем:

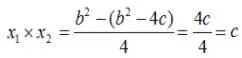
Таким образом, оба равенства теоремы Виета доказаны.

Формулировка обратной теоремы Виета:

Если числа x 1и x 2таковы, что их сумма равна второму коэффициенту уравнения x 2+ bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x 2+ bx + c = 0.

Доказательство обратной теоремы Виета читатели могут произвести самостоятельно.

1. x 2– 28 x + 171 = 0

2. x 2+ 8 x – 180 = 0

3. x 2– 10 x – 75 = 0

4. x 2+ 22 x + 72 = 0

5. x 2+ 0 x – 289 = 0

6. x 2– 6 x – 160 = 0

7. x 2+ 1 x – 30 = 0

8. x 2– 2 x – 120 = 0

9. x 2– 14 x + 40 = 0

10. x 2+ 7 x – 18 = 0

11. x 2– 6 x – 160 = 0

12. x 2+ 3 x – 10 = 0

13. x 2+ 6 x – 7 = 0

14. x 2– 20 x + 19 = 0

15. x 2+ 5 x – 50 = 0

16. x 2– 8 x – 9 = 0

17. x 2– 17 x – 38 = 0

18. x 2+ 7 x + 6 = 0

19. x 2+ 17 x + 30 = 0

20. x 2– 28 x + 160 = 0

21. x 2+ 30 x + 221 = 0

22. x 2+ 0 x – 16 = 0

23. x 2– 2 x – 120 = 0

24. x 2+ 4 x – 77 = 0

25. x 2+ 14 x + 45 = 0

26. x 2+ 19 x + 18 = 0

27. x 2– 23 x + 102 = 0

28. x 2+ 9 x – 90 = 0

29. x 2+ 9 x – 220 = 0

30. x 2– 5 x – 126 = 0

31. x 2– 25 x + 136 = 0

32. x 2– 20 x + 19 = 0

33. x 2– 1 x – 132 = 0

34. x 2– 17 x + 60 = 0

35. x 2+ 6 x – 7 = 0

36. x 2+ 15 x + 36 = 0

37. x 2+ 1 x – 240 = 0

38. x 2– 12 x + 27 = 0

39. x 2– 6 x – 135 = 0

40. x 2– 19 x + 70 = 0

41. x 2+ 9 x – 22 = 0

42. x 2+ 3 x – 10 = 0

43. x 2+ 20 x + 84 = 0

44. x 2– 9 x – 10 = 0

45. x 2+ 17 x + 52 = 0

46. x 2– 13 x – 114 = 0

47. x 2+ 3 x – 88 = 0

48. x 2+ 33 x + 260 = 0

49. x 2– 12 x + 36 = 0

50. x 2– 17 x + 0 = 0

51. x 2+ 25 x + 136 = 0

52. x 2– 18 x + 81 = 0

53. x 2– 9 x – 90 = 0

54. x 2+ 23 x + 60 = 0

55. x 2+ 25 x + 136 = 0

56. x 2– 15 x + 50 = 0

57. x 2+ 14 x – 120 = 0

58. x 2+ 5 x – 126 = 0

59. x 2– 7 x – 120 = 0

60. x 2+ 12 x – 45 = 0

61. x 2+ 26 x + 160 = 0

62. x 2+ 27 x + 162 = 0

63. x 2+ 1 x – 30 = 0

64. x 2– 6 x – 135 = 0

65. x 2+ 8 x – 105 = 0

66. x 2– 4 x – 45 = 0

67. x 2+ 15 x + 14 = 0

68. x 2– 4 x + 3 = 0