Журнал «Юный техник» - Юный техник, 2011 № 12

Работа руководителей факультативов может оплачиваться общеобразовательным учреждением как руководство профильными факультативными занятиями по предоставлении ФЗФТШ при МФТИ соответствующих сведений.

Руководители, работающие с учащимися, будут в течение учебного года: получать учебно-методические материалы (программы по физике, математике и информатике, задания по темам программ, решения заданий с краткими рекомендациями по оценке работ учащихся); приглашаться на курсы повышения квалификации учителей физики и математики, проводимые на базе МФТИ. Работы учащихся проверяют и оценивают руководители факультативных групп, а в ФЗФТШ ими высылаются ведомости с итоговыми оценками по каждому заданию и итоговая ведомость за год.

ОЧНОЕ ОТДЕЛЕНИЕ (обучение в вечерних консультационных пунктах)

Тел. (499) 755-55-80, e-mail: zftsh@mail.mipt.ru

Для учащихся Москвы и Московской области по программе ФЗФТШ работают вечерние консультационные пункты. Набор в них проводится по результатам вступительных экзаменов по физике и математике и собеседования, которые проходят в середине сентября. Обучение ведется по двум предметам.

Программы ФЗФТШ при МФТИ являются профильными дополнительными образовательными программами и едины для всех отделений.

Кроме того, ученикам всех отделений будет предложено участвовать в физико-математической олимпиаде «ФИЗТЕХ — 2012», которая, как правило, проводится на базе МФТИ и в ряде городов России в конце марта, в других очных и заочных олимпиадах МФТИ и его факультетов. Для учащихся 9 — 11 классов на базе МФТИ работает субботний лекторий по физике и математике по программе ФЗФТШ. Лекции читают преподаватели института (как правило, авторы заданий). Подробнее об этих мероприятиях можно прочитать на сайте ФЗФТШ: http://www.school.mipt.ru.

По окончании учебного года учащиеся, успешно выполнившие программу ФЗФТШ, переводятся в следующий класс, а выпускники (11 кл.) получают свидетельство об окончании школы с итоговыми оценками по изучавшимся в 11-м классе предметам. Ученикам, зачисленным в ФЗФТШ, будет предложено оплатить безвозмездный целевой взнос для обеспечения учебного процесса в соответствии с уставными целями школы.

Сумма взноса может ориентировочно (при обучении по двум предметам) составлять для учащихся заочного отделения 2000–3000 руб. в год, для очного 3500–6000 руб. в год, для очно-заочного — 2800–4500 руб. (с каждой факультативной группы) в год.

Для учащихся Украины работает УЗФТШ при ФТННЦ НАН Украины (обучение платное). Желающим поступить туда следует высылать работы по адресу: 03680, Украина, г. Киев, б-р Вернадского, д. 36, ГСП , УФЗФТШ. Тел: 8-(10-38-044) 424-30-25, 8-(10-38-044)422-95-64. Сайт УЗФТШ: mfti.in.ua, e-mail: ftcsch@imp.kiev.ua .

Для учащихся из зарубежных стран возможно только платное обучение на заочном и очно-заочном отделениях.

Внимание!Прислав нам решенное вступительное задание, вы даете согласие на обработку ваших персональных данных (в соответствии с Федеральным законом от 27.07.2006 г. № 152-ФЗ), которые будут использованы исключительно для отправки вам материалов по почте и учета вашей успеваемости.

Номера задач, обязательных для выполнения (заочное и очно-заочное отделения), приводятся в таблице:

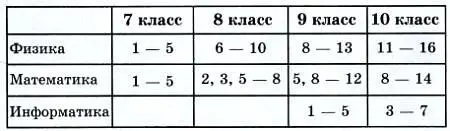
Номера классов указаны на текущий 2011–2012 учебный год.

МАТЕМАТИКА

1. Решите уравнение

(3х + 0,4) 2+ (4х + 2) 2— (5х+7/3) 2= 1 + 1/(4 — 31/64).

2. Поезд, двигаясь с постоянной скоростью, к 23.08 проехал в 1,35 раза больший путь, чем к 19.45 того же дня. Когда поезд выехал?

3. Заданы три точки: А(3;-4), В(-2;5), С(-12;3). Составьте уравнение прямой, проходящей через точку С и параллельной прямой АВ .

4. В треугольнике ABC биссектриса СЕ перпендикулярна медиане AM . Найдите АС , если ВС = 2012.

5. На первой остановке маршрута в пустой салон троллейбуса вошли пассажиры, и половина из них заняли места для сидения. Сколько человек вошло в троллейбус на первой остановке, если после второй остановки число пассажиров увеличилось на 8 % и известно, что троллейбус вмещает не более 70 человек?

6. В четырехугольнике PQSR противоположные стороны PQ и SR параллельны, а биссектрисы углов RPQ и SQP пересекаются в точке М , лежащей на отрезке RS . Найдите длину отрезка PR , если RS = 2012 км, QS = 458 км.

7. В треугольнике DEF проведена медиана DK . Найдите углы треугольника DEF , если известно, что угол KDE равен 70°, а угол DKF равен 140°.

8. Найдите количество трехзначных чисел, в каждом из которых сумма каких-либо двух цифр равна 3.

9. Угол BAD параллелограмма ABCD равен 60°; биссектрисы углов А и D этого параллелограмма пересекаются на прямой ВС . Найдите диагонали параллелограмма, если АВ = а.

10. При каких значениях параметра а уравнения

6х 2— (7а + 1)х — За 2= 4а + 1и х 2+ х + а = а 2

имеют общий корень?

11. Во время поездки по загородному шоссе автомобиль на каждые 100 км пути расходует на 3 л бензина меньше, чем в городе. Водитель проехал 48 минут по городу и 2 часа по загородному шоссе и затратил 27,2 л бензина. Затем водитель проехал по загородному шоссе еще полтора часа, затратив 15,6 л бензина. Найдите среднюю скорость автомобиля за всю поездку, если по городу автомобиль едет на 30 км/ч медленнее, чем по загородному шоссе.

12. Найдите значение выражения (cos 4a + sin 4a — 1)/(cos 6a + sin 6a — 1).

13. Решите уравнение cos12х: = cos6х + sin6х.

14. Даны геометрическая прогрессия с общим членом Ь n и арифметическая прогрессия с общим членом а n , разность которой отлична от нуля. Известно, что Ь 1= а 2 , b 2= а 14 , Ь 3= а 8 . Определите, являются ли четвертый и пятый члены геометрической прогрессии Ь 4 и Ь 5 также членами данной арифметической прогрессии (если да, то определите их номера).

ФИЗИКА

1. Каждый участник команды (в состав команды входят два школьника) должен пробежать в эстафете один круг по стадиону ( L = 400 м). Тренер находится у беговой дорожки на расстоянии l = 20 м по направлению движения от линии старта. Школьник, бежавший первый этап, пробежал мимо тренера через время t 1 = 4 с после старта. Второй участник команды преодолел свой (второй) этап эстафеты за время t 2 = 1 мин. 40 сек. Определите скорости школьников. Считать, что каждый из них бежит свой этап с постоянной скоростью. Определите среднюю скорость бега этой эстафетной команды.