Владимир Успенский - Апология математики, или О математике как части духовной культуры

Само слово «алгоритм» достаточно интересно: это, возможно, единственный математический термин, имеющий в своей этимологии географическое название. Таким названием служит слово «Хорезм». Великий учёный Мухаммед бен Муса аль-Хорезм и жил в конце VIII — первой половине IX века. Арабское имя «аль-Хорезми» буквально означает ‘из Хорезма’. Аль-Хорезми предложил некоторые методы решения арифметических задач, и на его авторитет ссылались средневековые европейские авторы, писавшие, как это было принято, на латыни. При этом начиная с XII века его имя транслитерировалось как «Algoritmi». Отсюда и пошёл термин «алгоритм». Поиски общего метода для решения массовой задачи велись со времён античности. Однако впервые ясное понимание алгоритма в качестве самостоятельной сущности встречается лишь в 1912 году в трудах великого французского математика Эмиля Бореля.

Понятие алгоритма — одно из центральных в математике. Программа для компьютера есть не что иное, как запись какого-то алгоритма на компьютерном языке. Прорыв в осознании этого важнейшего понятия произошёл в 1936 году, когда независимо друг от друга Алонзо Чёрч в Америке и Алан Тьюринг в Англии предложили математические уточнения понятия алгоритма (каждый своё) и на основе этих уточнений предъявили первые примеры массовых проблем, неразрешимых алгоритмически, в числе которых оказалась и очень знаменитая, стоявшая с 1915 года так называемая «das Entscheidungsproblem» («проблема разрешения»), считавшаяся главной проблемой математической логики. Поясним, что термины «проблема» и «задача» для нас синонимы и что массовая проблема считается алгоритмически неразрешимой, если не существует решающего её алгоритма, то есть такого единого алгоритма, который позволял бы находить решение для каждой из тех единичных проблем, которые и составляют рассматриваемую массовую проблему.

Алгоритмически неразрешимые проблемы, указанные Чёрчем и Тьюрингом, слишком сложны, чтобы их здесь формулировать. Сейчас мы приведём достаточно простой пример такой проблемы. Разумеется, мы вынуждены ограничиться её формулировкой и не приводить ни доказательства, ни даже намёка на доказательство её неразрешимости. Пример этот покажет, что массовые проблемы, для которых отсутствует требуемый алгоритм, лежат совсем близко к нашей повседневной жизни.

В целях большей наглядности изложим наш пример в терминах некоей игры. Любезный читатель согласится, что такая игра вполне мыслима в нашу эпоху пиара, рекламных акций, казино и игровых автоматов.

Средствами игры будут служить пластинки, наподобие тех доминошек, что используются при игре в домино. Как и в домино, каждая пластинка разделена на верхнюю и нижнюю половину. В каждой половине что-то написано. Отличие от домино в том, чт о именно написано. В случае домино в каждой из половин записывается количество очков, от 0 до 6. А нашем случае в каждой из половин записывается какая-то цепочка из букв икс и зет. Вот примеры таких цепочек. Цепочки длины один: x, z . Цепочки длины два: xx, xz, zx, zz . Цепочки длины три: xxx, xxz, xzx, xzz, zxx, zxz, zzx, zzz. Возможна и цепочка длины ноль, в этом случае не записано ничего. А вот одна из 128 цепочек длины семь: zxzxxxz . Проиллюстрируем сказанное примерами возможных пластинок:

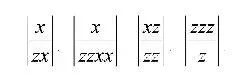
Перечисленные 4 пластинки, в том порядке, как они указаны, обозначим — для дальнейших ссылок — буквами A, B, C, D . Если приложить одну пластинку к другой, но не торцами, как при игре в домино, а боками, то в результате получим две строчки букв: одну сверху, другую снизу. Так, прикладывая A к D (слева D , справа A ), получаем zzzx сверху и zzx снизу. Если приложить в другом порядке, получим xzzz сверху, zxz снизу. Аналогично можно прикладывать друг к другу несколько пластинок и считывать верхнюю и нижнюю строчки букв. Более того. Каждую пластинку разрешается воспроизводить в неограниченном количестве и создавать сочетания из повторяющихся пластинок — такие, например, как AACA . В этом примере верхней строчкой будет xxxzx , а нижней — zxzxzzzx . Прошу у читателя прощение за затянувшееся предварение к игре, но хотелось бы, чтобы всё было предельно ясно.

Теперь — сама игра. Она состоит в следующем. В средствах массовой информации объявляется некоторый конкретный набор пластинок. Далее предлагается, воспроизводя каждую из пластинок набора в необходимом количестве, приложить пластинки друг к другу так, чтобы верхняя и нижняя строчки иксов и зетов совпали друг с другом. Первым пяти, приславшим решения, будет выплачен внушительный приз.

Поясним сказанное на примерах. Пусть объявленный набор содержит всего только одну пластинку A из приведённого выше перечня. Ясно, что решение невозможно, поскольку, сколько раз ни прикладывай пластинку A саму к себе, нижняя строка всегда окажется длиннее верхней. По сходной причине решения не существует, если объявленный набор состоит из одной только пластинки D , только тут длиннее будет верхняя строка. Желающие могут попытаться доказать, что решения не существует и в том случае, когда объявленный набор состоит из двух пластинок, A и D . А вот если объявить набор из всех наших четырёх пластинок A, D, C и D , то решение существует. Действительно, если сложить пластинки в таком порядке: DBCDA , то и верхняя, и нижняя строка окажутся одинаковы: zzzxxzzzzx .

Итак, набор объявлен. Все хотят получить приз. Но прежде, чем пытаться найти такое расположение пластинок, при котором верхняя и нижняя строки окажутся одинаковыми, желательно узнать, возможно ли такое расположение в принципе. Ведь если оно невозможно, то бесперспективно его искать, это будет пустой потерей времени. Так вот, оказывается, что не существует никакого эффективного способа это узнавать. Не существует (именно не существует, а не просто неизвестен) такого алгоритма, который позволял бы для любого объявленного набора пластинок узнать, имеется ли решение, то есть возможно или невозможно сложить пластинки требуемым образом. Для каждого отдельно взятого набора пластинок задача узнать, к какой из двух категорий этот набор относится — к той, для которой решения имеются, или же к той, для которой решений нет, — она, эта задача, есть сугубо творческая задача, своя для каждого такого набора, а общий метод получения ответа для всех таких задач отсутствует.