Владимир Успенский - Апология математики, или О математике как части духовной культуры

На языке лингвистики то, чем мы занимались в этой главе, есть семантика количественных числительных. При этом выяснилось, что привычный бесконечный ряд «конечных» числительных: один, два, три,…, сорок восемь,…, две тысячи семь,… — может быть дополнен «бесконечным» числительным алеф-ноль —

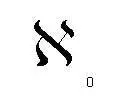
Но ведь бывают и числительные порядковые: первый, второй, третий и т. д. Вкратце поговорим и о них. Как количественное числительное есть словесное выражение (имя) количественного числа (оно же кардинальное число, оно же мощность ), так порядковое числительное есть словесное выражение (имя) порядкового числа . Чтобы отличать порядковые числа от количественных, будем обозначать их — в конечном случае (а про бесконечный мы пока ничего не знаем) — римскими цифрами, как это и принято в русской орфографии. Ведь мы пишем «Генрих VIII», а не «Генрих 8». Порядковое число — это особая сущность, для которой сейчас будет предложено не определение (что перегрузило бы изложение), а ассоциативная иллюстрация. С этой целью обращусь к своим детским ощущениям — ещё более ранним, чем кошмар, упомянутый в самом начале данной главы. В свои студенческие годы я с изумлением узнал, что эти ощущения испытал не только я.

Итак, раннее детство. Я размышляю, какой я плохой. Но тут же приходит в голову мысль, что раз я это понял, значит, я хороший. Но если я считаю себя хорошим, то, значит, я плохой. Но тогда я хороший — и так далее. Какую замечательную бесконечную лестницу я выстроил, хвалю я себя. Какой я плохой, что себя хвалю. И так далее. Здесь иллюстрация понятия порядкового числа. В самом деле, естественно называть ступени возникшей лестницы словами «первая», «вторая», «третья» и так далее. А можно сказать и так: со ступенями соотносятся порядковые числа I («я плохой»), II («я хороший, потому что осознал, что плохой»), III («я плохой, потому что себя похвалил») и так далее. С лестницей же в целом («я хороший, потому что смог увидеть всю лестницу») соотносится некоторое новое, бесконечное порядковое число (омега). Далее следуют + I («я плохой, потому что себя похвалил»), + II, + III и так далее. А потом, за ними всеми, + ω. Здесь мы остановимся, однако читатель волен продолжить это ряд и далее. Начиная с ω идут бесконечные порядковые числа . Их именами служат выражения «омега», «омега плюс один», «омега плюс два», «омега плюс три» и так далее. С семантической точки зрения эти выражения представляют собою порядковые числительные. С синтаксической точки зрения порядковые числительные должны быть похожи на прилагательные, и потому следовало бы говорить «омеговый», «омега плюс первый» и так далее; но так почему-то не говорят.

Читатель, желающий проверить себя на понимание бесконечных порядковых чисел (а автора — на способность понятно изложить), благоволит выполнить такое упражнение. Возьмите множество, состоящее из числа 3, числа 2, всех чисел 0, 1/ 2, 2/ 3, 3/ 4, 4/ 5и так далее и всех чисел 1, 1 1/ 2, 1 2/ 3, 1 3/ 4, 1 4/ 5и так далее. Занумеруйте элементы этого множества, в порядке их возрастания, порядковыми числами. Какие номера они получат? Ответ: первым, наименьшим элементом является здесь 0 и он получит номер I, элемент 1/ 2получит номер II, элемент 2/ 3получит номер III, и так далее; далее, элемент 1 получит номер, элемент 1 1/ 2получит номер + I, элемент 1 2/ 3получит номер + II, и так далее; наконец, элемент 2 получит номер + ω, и элемент 3 получит номер ++ I.

То, что общественное сознание отчасти мифологично, давно перестало быть новостью. Все знают, что во время Второй мировой войны, в период германской оккупации Дании, датский король надел жёлтую звезду. На самом деле этого не было. Всем известны слова Ленина, что искусство должно быть понятно массам, и сетования Пушкина на то, что он родился в России с умом и талантом. На самом деле Ленин (в беседе с Кларой Цеткин) говорил не «понятно массам», а «понято массами», а Пушкин (в письме к жене) писал не «с умом», а «с душою». Замена понятности на необходимость понимания и ума на душу в корне меняет смысл привычных формулировок. Если искажение слов Ленина можно списать на неправильный перевод с немецкого (а подлинник текста Цеткин был доступен в России единицам), то случай с Пушкиным требует более глубокого анализа. Объяснение состоит здесь, по-видимому, в том, что наше сознание готово допустить неуместность в России ума (которым, как известно, Россию не понять), но никак не души (это в России-то, этом заповеднике духовности и душевности!). Сила предубеждённости в этом вопросе поистине замечательна: ведь тираж изданий писем Пушкина исчисляется сотнями тысяч! Тем не менее ошибку в цитате делают даже филологи весьма известные. Вот ещё распространённый миф — формула Обещаю говорить правду, только правду и ничего, кроме правды , якобы применяемая в американском судопроизводстве (формула довольно странная, поскольку смысл оборотов «только правду» и «ничего, кроме правды» один и тот же). На самом деле в Америке говорят по-другому: «Обещаю говорить правду, всю правду и ничего, кроме правды, и да поможет мне Бог» (Promise to tell the truth, the whole truth, and nothing but the truth, so help me God).

Математика может чувствовать себя польщённой тем, что к числу деталей, в которых мифологическая картина мира отличается от картины реальной, принадлежат и некоторые математические сюжеты. Например, большинство убеждено, что в математике все понятия определяются и все утверждения доказываются. Но ведь каждое понятие определяется через другие понятия, а каждое утверждение доказывается, опираясь на другие утверждения. Вспоминается риторический вопрос г-жи Простаковой: «Портной учился у другого, другой у третьего, да первой портной у кого же учился?» Автору этих строк приходилось слышать и такое определение площади поверхности шара: «Площадь поверхности шара есть предел площадей поверхностей правильных многогранников, вписанных в этот шар, — при неограниченном возрастании числа граней этих многогранников». Подобное представление о площади поверхности явно возникло по аналогии с тем фактом, что длина окружности действительно есть предел периметров правильных многоугольников, вписанных в эту окружность, — при неограниченном возрастании числа сторон этих многоугольников. Но всё дело в том, что в правильном многоугольнике может быть какое угодно количество сторон, в правильном же многограннике количеством граней может служить лишь одно из следующих пяти чисел: четыре (у тетраэдра), шесть (у куба, он же гексаэдр), восемь (у октаэдра), двенадцать (у додекаэдра) или двадцать (у икосаэдра) — так что ни о каком неограниченном возрастании числа граней не может быть речи.