Вильгельм Оствальд - Искусство цвета. Цветоведение: теория цветового пространства

Приведенный выше геометрический ряд серых цветов начинается с идеально-белого цвета, который вполне определяется условиями полного отражения и рассеивания. Хотя И. Ламберт еще в XVII веке дал такое определение белому цвету и это определение нашло свое применение и в других отраслях науки, как, например, в астрономии, – для авторов, работающих в области науки о цветах, оно осталось но сей день чуждым. Даже Геринг приводит хорошо известный опыт (с отражением дневного света от посеребренного покровного стеклышка, лежащего на белой бумаге) – имеющий целью доказать, что белый цвет можно усиливать безгранично. Мы тут наталкиваемся на ошибочное смешение белого цвета с блеском. Посеребренное покровное стеклышко не рассеивает свет, а только отражает его; оно поэтому не белое, а блестящее.

Несколько иначе проявляет себя черный конец ряда. Первый, описанный нами выше, ахроматический ряд был расположен непосредственно по степеням светлоты и носит поэтому название аналитического ряда и заканчивается черным цветом со светлотой, равняющейся нулю. Такой черный цвет мы можем всегда воспроизвести в отверстии ящика, окрашенного изнутри в черный цвет. Не существует, однако, ни одного такого красящего вещества, которое дало бы этот черный цвет, в чем мы легко убеждаемся, когда сравниваем различные черные окраски с таким отверстием вычерненного внутри ящика. Составленный согласно закону Фехнера геометрический ряд выражает этот факт тем, что совершенно черный цвет является в нем бесконечно удаленным. Сколько бы мы ни продолжали этот ряд, всегда можно прибавить еще одну ступень, которая была бы меньше предыдущей в определенном количественном отношении.

На практике все-таки этот ряд имеет предел благодаря вышеозначенному свойству всех черных тел отражать всегда и некоторое измеримое количество белых лучей. Этот предел очень непостоянен и с развитием техники постепенно удаляется.

Здесь необходимо вспомнить также и о существовании порога ощущения, благодаря которому при известной силе света наше ощущение этого света уже прекращается, так как раздражение лежит ниже порога, а поэтому для нас неощутимо. Этим обстоятельством вызывается необходимость дать цветовому ряду законченный вид.

Тут же необходимо указать и на следующее: шкала серых цветов, изображенная в виде нисходящего геометрического ряда, представляет собой не один только «ряд Фехнера», а бесконечное множество таковых. Это происходит оттого, что таковой ряд выражает ведь не силу падающего света, но величины отражения. В зависимости от силы освещения, ступени шкалы будут давать самые различные количества света. В особенности при слабом свете – многие ступени конца черного ряда могут опуститься ниже порога и будут все выглядеть черными.

В этом можно убедиться, рассматривая такую шкалу в сумерках. При хорошем же свете даже ступени r и t находятся выше порога чувствительности и их можно легко отличить друг от друга.

Это и послужило причиной того, что при выработке шкалы мы пользовались исключительно законом Фехнера, не обращая внимания на порог чувствительности в темном конце. Включение этого обстоятельства оправдало бы себя только при определенном освещении, не говоря уже о существовании индивидуальных различий в величине порога. Шкала, предназначенная для общего пользования, не должна содержать этих переменных величин, если мы желаем, чтоб она была достаточно универсальна. Тот, кто пользуется шкалой, должен со своей стороны обратить внимание на то, какова средняя интенсивность освещения вокруг его рабочего стола. Сообразуясь с этим он и выбирает область шкалы, наиболее ему подходящую.

Несмотря на то, что вышеизложенные отношения между аналитической и психологической серой шкалой так просты, что для их объяснения не требуется рисунка, мы все-таки считаем полезным дать таковой. Это необходимо, потому, что в дальнейшем, в более сложном случае, с цветными треугольниками одинаковых тонов, нам придется делать подобные же передвижки, и если мы здесь познакомимся с более простым случаем, то в дальнейшем нам будет легче понять все излагаемое.

На рис. 4 левое деление представляет собою аналитическую гамму, разделенную на сто ступеней. Правое деление представляет собой точки acegilnprt практической шкалы серых цветов, расположенных соответственно содержанию в них белого цвета. Из рисунка видно, как велики расстояния ас и cl, как они быстро уменьшаются и в точках r и t так приближаются друг к другу, что становится невозможным нанести между ними еще какие-нибудь точки. Теоретически все-таки мы должны поместить между точкой t и конечной точкой еще бесконечное множество ступеней шкалы серого.

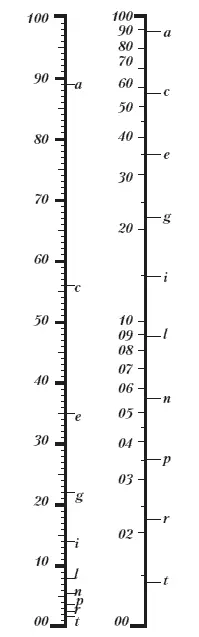
Рис. 4

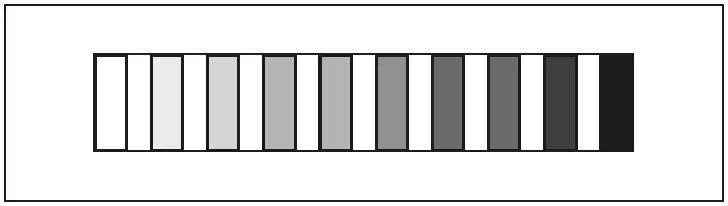
Рис. 5

Мы можем представить это изображение и в другом виде, расположив ступени серой шкалы, которые мы воспринимаем, как равно отстоящие друг от друга, на одинаковых расстояниях друг от друга, как то сделано на рисунке шкалы (рис. 5). В таком случае масштаб, обозначающий количество белого, мы должны уже нарушить так, что точки вблизи белого будут сближены друг с другом, точки же, лежащие к темному концу, – все больше раздвинуты. Левая сторона правого рисунка рис. 4 и изображает такие деления, которые соответствуют одинаковоотстоящим друг от друга, ступеням Фехнеровского ряда, написанным справа. Деления слева соответствуют логарифмической счетной линейке. В направлении сверху вниз они соответствуют нисходящему геометрическому ряду и повторяются между 10 и 01, так же как между 100 и 10, с той только разницей, что величины расстояния между ними здесь в десять раз меньше. Теоретически мы это деление можем продолжать до бесконечности, с интервалами от 01 до 001, от 001 до 0001 и так далее. Практически к этому прибегать не приходится, так как существует очень мало поверхностей, которые отражают меньше одной сотой доли падающего на них света. Здесь мы имеем, следовательно, изображенными графически, те самые отношения, о которых только что говорили выше. Такое деление, как на рис. 5, называется логарифмическим делением. Шкалу серых цветов, расположенную согласно закону Фехнера, тоже поэтому называют логарифмическим рядом или логарифмической шкалой. Такое логарифмическое деление всегда необходимо там, где закон Фехнера находит свое применение. Это касается особенно всякого рода нормировки, значение коей для работы и обихода необычайно велико. И самым ценным следствием внесения в науку о цветах меры и числа является именно возможность ныне нормировать весь мир цветов.