Даниил Хармс - Неизданный Хармс

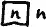
– поднятием числа n.

или поднятое n.

Для краткости можем вырожение

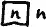
изображать просто так:

25 мая 1931 года.

♂ 2 августа 1932 года.

Курск.

«Безконечное, вот ответ на все вопросы. Все вопросы имеют один ответ. А потому нет многих вопросов, есть только один вопрос. Этот вопрос: что такое бесконечное?»

Я написал это на бумаге, перечитал и написал дальше:

«Безконечное, кажется нам, имеет направление, потомучто мы всё привыкли воспринемать графически. Большему соответствует длинный отрезок, а меньшему – короткий отрезок. Безконечное, это прямая, не имеющая конца ни в право, ни в лево. Нотакая прямая недоступна нашему пониманию. Если на идеально глатком полу, лежит глаткий, плоский предмет, то овладеть этим предметом мы можем только в том случае, если мы доберёмся до его краёв; тогда мы сможем поддеть рукой под край этого предмета и поднять его. Бесконечную прямую не подденешь, не охватишь нашей мыслею. Она нигде не пронзает нас, ибо для того чтобы пронзить что-либо, должен обнаружиться ее конец, которого нет. Это косательная к кругу нашей мысли. Ее прикосновение так не материально, так мало, что собственно нет никакого прикосновения. Оно выражается точкой. А точка, это бесконечно несуществующая фигура. Мы-же представляем себе точку, какбесконечно маленькую точечку. Но это ложная точечка. И наше представление о бесконечной прямой – ложное. Бесконечность двух направлений, к началу и к концу, настолько непостижима, что даже не волнует нас, не кажется нам чудом, и, даже больше, не существует для нас. Но бесконечность одного направления, имеющая начало, но неимеющая конца, или имеющая конец, но не имеющая начало, такая бесконечность потрясает нас. Она пронизывает нас своим концом или началом, и отрезок бесконечной прямой образующий хорду в кругу нашего сознания, с одной стороны постигается нами, а с другой стороны соединяет нас с бесконечным. Представить себе, что что то никогда не начиналось и никогда не кончится мы можем в искажённом виде. Этот вид таков: чтото никогда не начиналось, а потомуникогда и не кончится. Это представление о чём то есть представление ни о чём. Мы ставим связь между началом и концом и отсюда выводим первую теорему: что нигде не начинается, то нигде и не кончается, а что где то начинается, то гдето и кончается. Первое есть бесконечное, второе – конечное. Первое – ничто, второе-что-то».

Я записал это всё, перечёл и стал думать так: «Мы не знаем явления с одним направлением. Если есть движение в право, то должно быть и движение в лево. Если есть направление вверх, то оно подразумевает в себе существование направления вниз Всякое явление имеет себе обратное явление. Всякая теза – антитезу. Что бесконечно вверх, то бесконечно вниз. [1]И до сего времяни, 1932 года, в природе этот закон не был нарушен. Мы не видим предела повышения температур, но мы видим предел понижения, это абсолютный нуль, температура – 273°. Но до сих пор мы её не достигли. Как бы близко мы к ней не приближались, мы её не достигли И мы не знаем, что случается с природой, когда она достигает этого предела. Тут очень интересное положение: чтобы достигнуть нижнего предела надо предпологать существование верхнего предела. В противном случае пришлось бы сделать следующие выводы: либо верхний предел где-то всё-же имеется, но пока нам ещё не известен, либо температура – 273° не есть нижний предел, либо достигнув нижнего предела природа видоизменяется настолько, что фактически перестает быть, либо теорема о концах бесконечности неверна. В последнем случае положение: „что то никогда не начиналось и никогда не кончится“ не может быть рассматриваемо как „чтото никогда не начиналось, а потомуникогда и не кончится“, и бесконечность двух направлений перестала бы быть ничем, а стала-бы чем то. Мы поймали-бы бесконечность за хвост».

Я написал это с некоторыми перерывами, потом перечитал это с большим интересом и продолжал размышлять так:

«Вот числа. Мы не знаем, что это такое, но мы видим, что по некоторым своим свойствам они могут распологаться в строгом и вполне определёном порядке. И даже многие из нас думают, что числа есть только вырожение этого порядка, и вне этого порядка существование числа – бессмысленно. Но порядок этот таков, что началом своим предпологает единство. Затем следует единство и ещё единство. Затем единство, еще единство и ещё единство и т. д. без конца. Числа вырожают этот порядок: 1, 2, 3 и т. д. И вот перед нами модель бесконечности одного направления. Это неуравновешенная бесконечность. В одном из своих направлений она имеет конец, в другом конца не имеет. Что то где то началось и нигде не кончилось, и пронзило нас своим началом, начиная с единицы. Несколько чисел первого десятка уложилось в кругу нашего сознания и соединило нас с бесконечностью. Но ум наш не мог вынести этого, мы уравновесили бесконечный числовой ряд другим бесконечным числовым рядом, созданным по принципу первого, но расположенным от начала первога в обратную сторону. Точку соединения этих двух рядов, одного естественного и непостижимаго, а другого явно выдуманного, но объясняющего первый, – точку их соединения мы назвали НУЛЬ. И вот числовой ряд нигде не начинается и нигде не кончается. Он стал ничем. Казалось бы всё это так, но тут всё нарушает нуль. Он стоит где то в середине бесконечного ряда и качественно разнится от него. То, что мы назвали ничем, имеет в себе ещё что-то, что по сравнению с этим ничем есть новое ничто. Два ничто? Два ничто и друг другу противоречивые? Тогда одно ничто есть чтото. Тогда чтото, что нигде не начинается и нигде не кончается, есть что то, содержащее в себе ничто».

Я прочитал написанное и долго думал. Потом я не думал несколько дней. А потом задумался опять. Меня интересовали числа, и я думал так:

«Мы представляем себе числа как некоторые свойства отношений некоторых свойств вещей. И, таким образом, вещи создали числа».

На этом я понял, что это глупо, глупо моё рассуждение. Я распахнул окно и стал смотреть на двор. Я видел, как по двору гуляют петухи и куры.

♂ <���вторник> 2 августа 1832

Трактат о красивых женщинах лежащих на пляже под Петропавловской крепостью, сидящих на Марсовом поле и Летнем Саду и ходящих в столовую Ленкублита

писан Даниилом Протопластом.

1133 год. Июль.

Эпиграф из тигров: «О фы! О фе!»

Кра кра краси фаси перекоси. Предмет, предмет, предмет, предмет, предмет, предмет, предмет, предмет, премет, предмет, предмет, предмет.