Даниил Хармс - Неизданный Хармс

Мы повесили сапог на ширму

Несколько лет, заполненных войной и революцией, заставили долгое время все население СССР думать лишь о том, как бы остаться живым и сытым. Год 1919 и 1920 был кульминационной точкой этого обжорного стремления. Человек есть борец за свое существование – значило буквально. С окончанием войны и революции обжорное напряжение стало ослабевать, но ему взамен наступил материализм в самой резкой форме, как следствие революции. Он постепенно спускался все в более низшие классы, одновременно с этим искажаясь и прикрывая собой романтическую сторону жизни. Установка всех суждений встала. Художественный гений потерпел обратный ход лозунгов: «Гений есть самобытность», «гений есть терпение и усидчивость». Всякое искусство и развлечение без непосредственной пользы в том стало преследоваться. Отсутствие отдыха путем разнообразия напряженности привело нас к усталости…

Теперь, когда не приходится думать только о наполнении своего желудка, все чаще и чаще слышится тоска о душевном разгуле. И вот ленинградская организация левого фронта искусства предлагает обществу свои услуги МЕТОДОМ ПОДТАСОВКИ. В СССР завал вульгарным материализмом, стремящимся сковать вольные движения человека осмыслицы и лишить его отдыха. Мы, истинные художники, доктора общественного желудка, дадим вам слабительную жижицу в виде хляпа крышки романтизма. Для нашего же интереса и отдыха мы создаем бюро «романтики и приключений» с неожиданным выкриком «Нужно жить очаровательно» и «не бей по сапогу – ширма свалится»

Август 11 1925 r.

Установим текучий слова для обозначения наиболее мелких камушков. Вся трудность нашего рассуждения будет заключатся в недоверии читателя к мыслям о картах человеческой глупости. Эта область колышится в нашем обеде, проникает в наши жилища, создает сны и очень часто разламывает дорогу неправельно посланных голубей из книги в общественный сад. Командир глупости

<1929–1930>

Поднятие число

Будем изображать велечины:

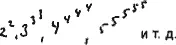
Понимай так:

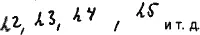
велечину:

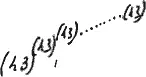
где количество степенных показателей (h3) равно основанию (h3)

будем изображать

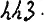
Понятно. что означает

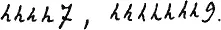
или, что тоже самое:

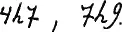
Допустим, что этих h не 7, как в последнем случае, а h8, тогда изобразим некое число, с корневым основанием 9 так:

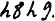
Будем называть 9 – корневым основанием, h стоящее перед корневым основанием титлом, выражение h8 назовем первый коэфициент титла.

Но мы можем увеличить все титулованное вырожение увеличив лишь коэфициент титла хотя бы так:

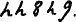
или ещё лучше так:

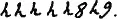
или что тоже самое:

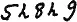
Тут 5 будет являться вторым коэфициентом титла. Однако мы можем титуловать и второй коэффициент титла, т. е.:

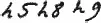
Тут вторым коэффициентом титла будет

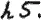
Рассуждая так дальше мы можем получить скажем такое выражение

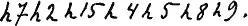
Возмём выражение где все коэффициенты титла выглядят одинаково (hm).

Вот:

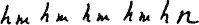
(где n коренноеоснование).

Мы можем это выражение записать проще, а именнотак:

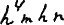
или ещё проще:

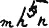
или общий случай

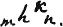
где k мы будем называть чином.

Рассмотрим случай титулования, где числа титулоых коэффициентов равны друг другу и равны кореному основанию:

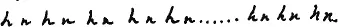
Если всех коэффициентов f, а f + 1 =k

гы мы это вырожение можем записать так:

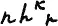
Если k = n, то

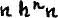
или просто:

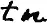
Это есть чинование n

Будем процесс титулования n изоброжать так:

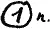
А процесс чинования n изображать так:

То легко себе представить процесс:

А так же:

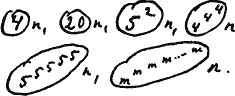
и наконец:

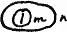
Возможны и такие случаи:

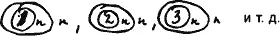
Изобразим это так

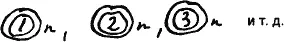
Возмём случай:

Легко представить как число колец будет рости. И когда достигнет n изобразим полученное выражение так:

Число квадратов так же может достигнуть n. Изобразим это так:

И так можно продолжать без конца. Круг был у нас первой сменой фигур, квадрат-второй, трехугольник – третей и т. д. Но будем квадрат всегда считать n-ой сменой фигур.

Поэтому выражение:

будет иметь определённое значение и мы будем называть: