Дмитрий Сочивко - Расколотый мир. Опыт анализа психодинамики личности человека в экстремальных условиях жизнедеятельности
- Название:Расколотый мир. Опыт анализа психодинамики личности человека в экстремальных условиях жизнедеятельности
- Автор:
- Жанр:
- Издательство:Литагент «Когито-Центр»881f530e-013a-102c-99a2-0288a49f2f10
- Год:2002
- Город:М.
- ISBN:5-9292-0079-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дмитрий Сочивко - Расколотый мир. Опыт анализа психодинамики личности человека в экстремальных условиях жизнедеятельности краткое содержание
В книге изложены теоретические и экспериментальные основания психодинамического подхода в исследованиях личности. Представление личности как ансамбля психодинамических циклов элементарных состояний волевой, эмоциональной и когнитивной сфер позволяет увидеть специфичность поведения человека в различных по экстремальности условиях жизнедеятельности. Книга интересна широкому кругу читателей, специалистов в области философии, антропологии теоретической и прикладной (в первую очередь социальной и юридической) психологии.
Расколотый мир. Опыт анализа психодинамики личности человека в экстремальных условиях жизнедеятельности - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
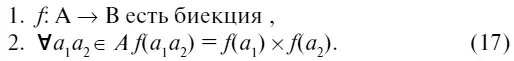
Такое отображение называется изоморфизмом. Если, однако, отображение f не биективно, а сюрьективно, то оно называется гомоморфизмом. В этом последнем случае абстрактная модель уже не полно отражает модель-объект. Тем не менее чаще всего с этим приходится мириться, так как добиться изоморфизма моделей бывает очень трудно или невозможно.
Среди алгебр крайне важными являются такие структуры с двумя заданными внутренними операциями. Пусть на множестве определены операции сложения и умножения, которые ставят в соответствие любой паре элементов множества соответственно их сумму и произведение, это множество называется кольцом, если: 1) относительно операции сложения исходное множество образует абелеву группу; 2) действие операции умножения над исходным множеством удовлетворяет закону ассоциативности: а × bс = ab × c ; 3) две операции связаны между собой законом дистрибутивности:
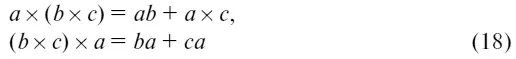
1.4. Линейные пространства
Пусть имеется множество М , состоящее из элементов произвольной природы. Пусть также над этим множеством задана операция сложения, и относительно этой операции данное множество М образует абелеву группу (группа относительно операции сложения часто также называется аддитивной группой или модулем). Если при этом имеется также некоторое поле К, элементы которого будут называться скалярами или коэффициентами, и определено умножение элементов К на элементы М , удовлетворяющее следующим требованиям. Для любых ∀ х, у ∈ М и a,b ∈ K: 1) хa лежит в М ; 2) ( х + у ) а = ха + уа ; 3) х ( а + в ) = ха + хв; 4) х 1 = х ; 5) х ( ав ) = ( ха ) в . Множество М в таком случае называется линейным пространством. В линейном пространстве операция умножения является внешней операцией. Таким образом, каждый элемент пространства может быть представлен уже не только как комбинация каких-то его элементов, но и как результат некоторого внешнего действия на какой-то его элемент. Очевидно при этом, что результат внешнего действия обязательно лежит в М .
Приведем некоторые важнейшие примеры задания линейных пространств.
Пусть множество векторов задано в трехмерном евклидовом пространстве. Два вектора считаются равными, если равны их длины, а сами векторы направлены в одну и ту же сторону. Нулевым вектором является вектор нулевой длины. Сложение векторов производится по правилу параллелограмма, умножению на скаляр соответствует растяжение вектора. В качестве поля скаляров используется поле действительных чисел. Легко проверить, что заданное множество векторов относительно операции сложения образует модуль, а операция умножения на действительное число удовлетворяет перечисленным требованиям.
Пусть множество М состоит из всевозможных упорядоченных наборов действительных чисел по k чисел в каждом. Упорядоченность набора означает, что числа определенным образом занумерованы, при этом они, однако, не обязаны быть различными. Пусть элемент х ∈ М задан набором х = { х 1, х 2…. х к}, а элемент у = { у 1, у 2, …, у к}. Элементы х и у будут равны в том и только в том случае, если х 1= у 1, х 2= у 2, …, х к= у кОпределим линейные операции в М следующим образом:
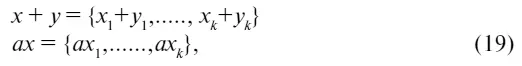
где а – коэффициент из поля действительных чисел. Нулевым элементом в множестве М является набор 0 = {0,…, 0} противоположным элементом элемента х является элемент – x = {— х 1, ………, – х k} Легко видеть, что множество М образует аддитивную группу. Предоставляем читателю проверить, что умножение наборов действительных чисел на действительное число по правилу (19) удовлетворяет требованиям 1)—5). Таким образом, множество М образует линейное пространство. Такое пространство является хорошей моделью психологического теста в его статическом варианте. Пусть имеется некоторое множество заданий (вопросов или утверждений), называемых тестовыми пунктами, и множество людей, называемых испытуемыми, которые, указывая некоторое действительное число, выражают степень своего согласия с утверждением тестового пункта (либо другие люди, называемые экспертами, указывают степень выполнения задания). Обычно для ответов испытуемым предлагается заранее заготовленный набор (целых) чисел, например от единицы до пяти или десяти, иногда также для ответа предлагается отрезок прямой, на котором испытуемый точкой отделяет часть, соответствующую степени его согласия. Тем или иным способом каждому испытуемому в результате тестирования ставится в соответствие набор действительных чисел, упорядоченный в соответствии с порядком предъявления испытуемому тестовых пунктов. Далее наборы, полученные для всех испытуемых, складывают по правилу (19). Полученный в результате сложения набор умножается на коэффициент, равный единице, деленной на количество испытуемых, подвергшихся тестированию. Таким образом, полученный набор называют психологической нормой теста для данной группы испытуемых. Если противоположный норме набор сравнить с набором, полученным в результате ответов конкретного испытуемого, то полученный результат называется характеристикой данного испытуемого в данной группе по данному тесту. Если протестированная группа испытуемых достаточно велика и разнообразна (со статистической точки зрения), т. е. является репрезентативной относительно генеральной совокупности, то можно говорить просто о характеристике испытуемого по тесту.
Итак, результаты психологического тестирования представляют собой векторы (упорядоченные наборы чисел также иногда называют k -мерными векторами) некоторого линейного пространства. Это линейное пространство в свою очередь, рассматривается как пространство того психологического свойства, которое подверглось тестированию. Результаты оформляются в виде таблицы.
Такая таблица называется матрицей. Обычно используют также сокращенную запись

При сложении матриц складываются числа с равными индексами (расположенные на одних и тех же местах). При умножении каждое число матрицы умножается на скаляр с из поля действительных чисел. Пространство матриц имеет широкое применение при обработке данных социально-психологического исследования.
Читать дальшеИнтервал:
Закладка:










