Дмитрий Сочивко - Расколотый мир. Опыт анализа психодинамики личности человека в экстремальных условиях жизнедеятельности

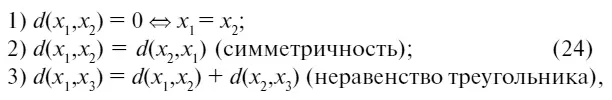
где x 1 , x 2 , x 3– произвольные элементы множества X .

Функцию d называют метрикой или расстоянием в X .

Само метрическое пространство есть, таким образом, пара ( X,d ). Очевидно, что структура метрического пространства полностью определена тем, как задана в нем функция расстояния или метрика. Заметим, что из неравенства треугольника, если положить х 1= х 3, следует, что d ( х 1 , х 2) ≥ 0. Таким образом, функция расстояния принимает только неотрицательные значения. Приведем некоторые примеры.

Множество действительных чисел является метрическим пространством, если определить расстояние между двумя числами равным абсолютной величине их разности: d ( х 1 х 2) = ( х 1– х 2). На множестве R n обычно вводят одну из следующих метрик:

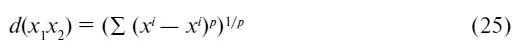
где р ≥ 1. Подставляя различные значения р в (25) мы можем получать различные метрики в пространстве R n , в том числе и метрику плоскостных изображений, в случае если

Метрика (26) называется евклидовой метрикой. Метрическое пространство R 3с евклидовой метрикой является моделью непосредственно окружающей человека физической среды.

Метрические пространства как модели социально-психологических явлений являются весьма мощным аппаратом представления в компактном и наиболее удобном для дальнейшего исследования виде больших массивов экспериментальных данных, а также позволяют учитывать сложные взаимовлияния большого числа элементов изучаемых систем. Важнейшими характеристиками таких моделей являются размерность пространства, его метрика и наличие или отсутствие структуры. Типичными примерами таких моделей в психологии являются пространства образов, пространства мнений или суждений, при этом подразделяют пространства коннотативных и денотативных суждений, факторные пространства личности. Эти последние обычно удовлетворяют требованиям линейности. В последнее время также активно исследуются пространства образов (методы с использованием «Семантического дифференциала» и другие) с привлечением методов многомерного статистического анализа. Отметим, что в социально-психологических исследованиях расстояния между образами устанавливаются в процессе обработки данных экспериментального шкалирования объектов по каждому из признаков. При этом взаимодействие признаков рассматривается как артефакт. В предлагаемом же в этой книге подходе именно это взаимодействие (собственно психодинамика) и является основным предметом исследования.

Очень часто при анализе сложных объектов действительности на первый план выдвигаются не метрические соотношения их элементов, расстояния между элементами, а отношения последовательности, соседства и т. п. Так в уже приведенном примере модели языка возможно, конечно, построение метрического пространства на основе так или иначе определенного расстояния между словами. В психосемантике такие модели имеют широкое распространение. Однако, если предметом анализа будет некоторый текст, написанный на данном языке, то более важным, чем расстояние между словами, моментом является порядок следования слов. Учитывая же, что в грамматике естественного языка правила допускают существенные вариации порядка слов, в качестве продуктивного понятия для анализа текста можно выдвинуть понятие окрестности слова в тексте, что и было в свое время сделано Ю.А. Шрейдером. Для того, чтобы точно определить понятие окрестности элемента некоторого множества, это множество необходимо наделить структурой топологического пространства, или топологией.

Говорят, что множество X наделено топологией или что множество Х есть топологическое пространство, если указана система Т подмножеств Х , обладающая следующими свойствами:

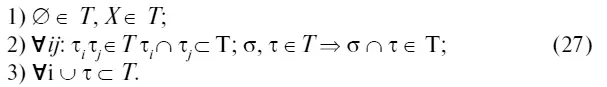
Семейство подмножеств Т называется топологией пространства Х и, как видно из (31), содержит пустое множество и само Х , а также содержит пересечение любой пары своих подмножеств и объединение любой пары своих подмножеств. Топологическое пространство, таким образом, есть пара ( X,Т ), при этом подмножества системы Т называют открытыми подмножествами, а все дополнения к ним называют замкнутыми подмножествами пространства X .

Теперь мы можем дать определение окрестности элемента x ∈ X (элементы х топологического пространства обычно называют точками). Окрестностью точки х топологического пространства ( X,T ) называют открытое множество, содержащее эту точку.

Задание топологии посредством перечисления всех подмножеств системы Т является делом весьма сложным и практически не всегда выполнимым. Обычно ограничиваются заданием некоторого небольшого числа подмножеств Х , объединением которых можно получить любое открытое подмножество X . Если это действительно достижимо, то такое семейство открытых подмножеств называют базой топологии над Х . Число подмножеств минимальной базы называют также весом топологического пространства. Ясно, что система всех окрестностей всевозможных точек Х может служить базой. Обратно, если над Х задана топология, то для каждой точки Х определена система окрестностей.

Всякое метрическое пространство наделено также и структурой топологического пространства. Однако пространства с различной метрикой могут, вообще говоря, обладать одной и той же топологией. Из этого позже читатель сможет сделать вывод, что разные с точки зрения метрических тестов (Кеттел, ММРI…) личности могут обладать одной и той же психодинамикой.

Кроме уже приведенного примера из математической лингвистики топологические пространства как модели психологических явлений широко используются в психосемантике и психологии личности. Обычно решаемая задача бывает одна и та же – определение минимальной базы топологии, которая затем рассматривается либо как глубинная семантическая структура, порождающая ее остальное множество значений, либо как глубинная психологическая структура, порождающая затем все многообразие личностей или все многообразие поведения конкретной личности в каких-то фиксированных условиях. Задача психодинамического подхода – показать реальную психодинамику на топологическом уровне, которая обеспечивает все многообразие личностных свойств.