Юрий Фомин - Энциклопедия аномальных явлений

Гипотеза о многомерности пространства требует возможности, для формирования четвертого измерения, переместить объем по четвертой координате, но как это сделать? Наше воображение отказывается представить себе такую возможность, оно монополизировано тремя пространственными измерениями, а дня четвертого просто не остается места.

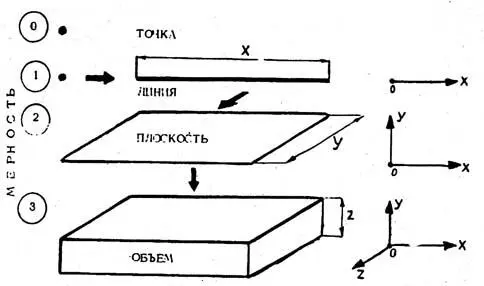
Рис. 3. Взаимосвязь между системами измерения.

Но, как уже указывалось, мерность не является объективной реальностью, а только формой ее восприятия и тесно связана с нашими возможностями восприятия окружающего мира, пределом осознаваемой мерности. Если мы не можем представить себе существование высших измерений, то это не может служить доказательством невозможности их существования. Пытаясь разрешить эту проблему, немецкий физик и физиолог Герман Гельмгольц (1812–1894) предположил, что есть существа, которые, в отличие от нас, способны осознавать только два измерения, и предложил рассмотреть взаимосвязь между пространственными измерениями. Эти гипотетические существа были названы "плоскатики". Данный прием позволяет — по аналогии взаимоотношения плоскатика с высшим для него третьим измерением — прояснить наши взаимосвязи с недоступными к нашему восприятию четвертым, пятым и т. д. пространственными измерениями.

Для плоскатика весь мир, доступный его восприятию, ограничивается только плоскостью, в которой он обитает. Он не может воспринимать что-либо находящееся за пределами этой плоскости. Для нас таким пределом является объем.

Таким образом, многомерность может рассматриваться с позиций геометрической и физической. Геометрическая концепция многомерности достаточно хорошо разработана и рассматривается как абстрактный, чисто математический прием, который не обязательно должен иметь физическую аналогию. Геометрическая многомерность используется при решении определенных конкретных инженерных задач и в ряде случаев, позволяет получить полезные результаты. Так, например, она успешно используется при исследовании разного рода многокомпонентных систем, где каждое измерение рассматривается как определенный показатель системы, а в совокупности n-мерный график позволяет выявить состояние системы в зависимости от комплексного измерения всех составляющих.

Совершенно иначе обстоит дело с физической трактовкой многомерности, которая, по крайней мере в отношении макро- и мегамиров, не признается большинством физиков. Однако разработанность геометрического представления о многомерности значительно расширяет возможности исследования физической многомерности, так как позволяет использовать математический аппарат и методические разработки.

Таким образом, геометрическая многомерность может, подсказать ожидаемые результаты физических исследований и наблюдений, а также указать наиболее рациональные пути проявления физической многмерности в природе.

Непосредственное познание физической многомерности невозможно при тех средствах восприятия окружающего мира, которым мы располагаем. Поэтому постараемся подойти к этой проблеме несколько иначе. Рассмотрим взаимосвязи между известными нам системами измерения (одномерными, двухмерными и трехмерными), выявим общие закономерности, которые определяют взаимосвязи между ними, и сформулируем их в виде постулатов.

Можно предположить, что эти постулаты окажутся справедливыми и при переходе от известного нам трехмерного мира к недоступным высшим измерениям. Таким образом окажется возможным выявить проявления многомерности в нашем трехмерном мире. Кроме того, появится возможность прогнозирования и объяснения некоторых явлений, не понятных в рамках общепринятого четырехмерного континуума.

Постулат 1. Любая система высшего измерения может содержать бесчисленное множество независимо существующих систем низшего измерения. Действительно, на плоскости можно разместить сколько угодно линий, а в объеме — сколько угодно плоскостей. Исходя из этого постулата, можно предположить, что четырехмерная система может содержать бесчисленное множество независимо существующих трехмерных систем или в нашем представлении — миров.

Постулат 2. Всякое понятие о расстояниях справедливо только в данной системе измерений; при переходе к высшим системам измерения расстояние между двумя любыми точками может быть сведено к нулю или к бесконечно малой величине.

Этот постулат можно проиллюстрировать таким примером. На плоскости расстояние между точками А и В вполне определенно (рис. 4), если эту плоскость изогнуть в третьем измерении, то точки можно совместить, хотя при этом расстояние между ними в плоскости не изменяется. Разность расстояния между двумя точками может иметь место и в разных системах одного и того же порядка, если они пересекаются. Такой пример приводится на рис. 5. В этом случае расстояние между точками М и К будут разными в независимых двухмерных системах А и В.

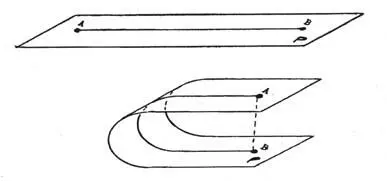
Рис. 4. Изменение расстояния между двумя точками при переходе от двухмерной системы к трехмерной

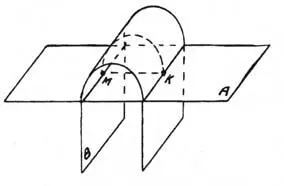
Рис. 5. Разность расстояний между двумя точками в разных системах измерений одного и того же порядка.

Постулат 3. Любая пространственная система может быть искривлена без какой-либо деформации только в высшей системе измерения, причем это искривление может быть обнаружено только в высшей системе измерения и не проявляется в низшей.

Это значит, что линию (одномерную систему) можно искривить только в плоскости (двухмерной системе), а плоскость — только в объеме (трехмерной системе), при этом расстояния между любыми точками низшей системы сохраняются неизменными в мой системе при искривлении ее в высшем измерении. Искривить плоскость в плоскости невозможно, это неизбежно приведет к деформации элементов системы.

Еще одна любопытная деталь, имеющая прямое отношение к этому постулату. Представим себе, что выдуманного Гельмгольцем плоскатика мы поместим на поверхность шара. Для него, осознающего только два измерения, шар будет представляться ровной поверхностью, так как он не в состоянии обнаружить его кривизну в третьем измерении. Перемещаясь все время только прямолинейно и только вперед, плоскатик в конечном счете вернется в ту же точку, откуда начал свое движение, только с обратной стороны. Для него это будет совершенно не понятным парадоксом.