Юрий Фомин - Энциклопедия аномальных явлений

Не исключено, что нечто подобное имеет место и с нами, если предположить, что хорошо знакомый нам трехмерный мир в действительности представляет собой кривую поверхность в четвертом измерении. Некоторые астрономические наблюдения позволяют предположить, что это предположение недалеко от истины.

Постулат 4. Физические тела могут проявляться в разных системах измерения, причем чем ниже система измерения, тем меньший объем информации она несет. Сложные объекты проявляются в низших измерениях в виде следа, проекции и сечения.

Представим себе некоторое объемное, трехмерное тело и попытаемся поместить его в двухмерную систему. Однако сделать это невозможно, можно только получить на плоскости некоторое сечение этого тела, в какой-то степени отражающее его форму и сущность. Это сечение будет напоминать чертеж объемного тела, но только в одной проекции.

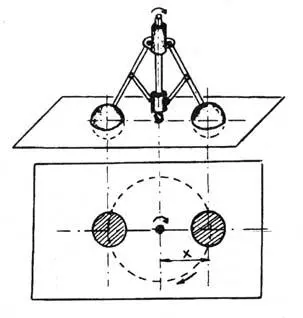
Рис. 6. Трехмерное тело в плоскости.

Предположим, что в качестве такого тела будет использован центробежный регулятор, причем в плоскость сечения попадут его ось и грузы (рис. 6). Плоскатики, обитающие в этой двухмерной системе, исследуя эти объекты, не смогут обнаружить видимой связи между этими тремя независимо существующими телами. Они смогут констатировать факт, что скорость вращения грузов и расстояние от оси до центров грузов (х) зависят от скорости вращения. Но почему? Этого плоскатики объяснить не могут, так как механизм системы не известен им. По всей вероятности, для описания этого явления им пришлось бы ввести некоторые условные понятия, аналогичные нашим понятиям "поле" или "взаимодействие", которые отражали бы реальную действительность, но не объясняли бы природы явлений.

Не пытаясь что-либо утверждать, отметим только, что описанная аналогия очень напоминает проявление полей и взаимодействий. Не исключено, что объяснение природы этих явлений следует искать именно в проявлениях многомерности. Это позволяет сформулировать следующий постулат многомерности.

Постулат 5. Чем выше мерность системы, тем большей информационной емкостью она обладает. Справедливость этого утверждения подтверждается данными, приведенными в таблице 1.

Постулат 6. Система низшего измерения любого порядка в высших измерениях может свертываться в точку без нарушения ее целости, при этом все точки низшей системы, сохраняя свое взаиморасположение, оказываются совмещенными.

Рассмотрим этот постулат на конкретных примерах. Одномерная система представляет собой линию, имеющую только одно измерение — длину. На плоскости этой линии можно придать любую конфигурацию, следовательно, она может быть свернута в спираль с бесконечно малым диаметром, т. е. практически сведена к точке. В этом случае все точки на линии будут находиться друг от друга на бесконечно малом расстоянии, причем целостность одномерной системы не будет нарушена.

Та же операция может быть выполнена и в системах высших измерений. Предположим, что существует двухмерная система, представляющая собой плоскость, на которой размещаются три, не связанные друг с другом фигуры (рис. 7). Свернем эту плоскость в третьем измерении и получим трубку бесконечно малого диаметра, так как двухмерная система не имеет толщины. Поэтому если число витков трубки будет стремится к бесконечности, то ее диаметр — к нулю. Плоскость превращается в линию. o

Трубку можно согнуть в кольцо; если ее концы вдвигать друг в друга, то диаметр кольца будет сокращаться, в результате образуется тор с бесконечно малым диаметром. Эта фигура будет стремиться к точке. В результате таких трансформацией расстояния между любыми точками на плоскости в третьем измерении будут сведены к бесконечно малой величине. Все независимые плоские фигуры окажутся совмещенными и образуют единое целое, хотя структура и метрические соотношения двухмерной системы останутся без изменения.

Можно предположить, что такие же закономерности сохранятся при переходе от трехмерной системы к четырехмерной, от четырехмерной к пятимерной и т. д.

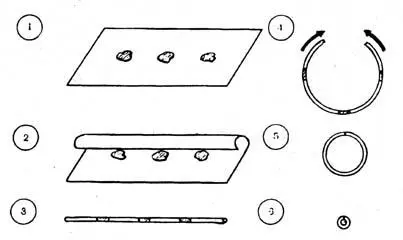
Рис. 7. Свертывание пространства в высших измерениях.

Для некоторого пояснения сказанного необходимо ввести точное разграничение понятий "искривление" и "деформация" пространства. Искривление пространства предполагает сохранение всех метрических соотношений между элементами пространства. Это значит, что расстояние между любыми двумя, произвольно взятыми точками в данном пространстве, остается неизменным при его искривлении в высшем измерении. Этот случай иллюстрируется рис. 8.

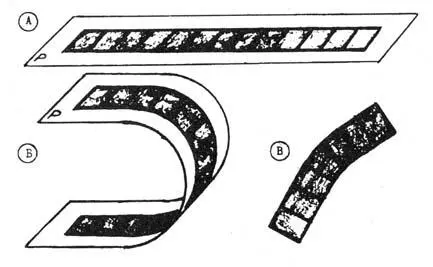
Рис. 8. Искривление и деформация пространства.

На двухмерной плоскости Р размещается плоское тело (рис. 8, А). Если эту плоскость искривить в третьем измерении (рис. 8, Б), то все расстояние между любыми двумя точками этого тела сохраняются. При попытке же искривить двухмерную фигуру в пределах двухмерной системы неизбежно произойдет деформация фигуры, ее метрические характеристики изменятся (рис. 8, В).

Приведенные примеры очень условны и могут рассматриваться только как упрощенные аналогии, позволяющие уяснить принципы изменения характеристик пространства в зависимости от мерности его восприятия. В действительности реализация этих свойств проявляется значительно сложнее, тем более в несших измерениях.

Нужно также учитывать и то, что реализация постулатов многомерности осуществляется не какими-то преднамеренными, посторонними силовыми воздействиями, а отражает существующую в независимости от нас объективную реальность. Постулаты позволяют уяснить, какие варианты проявления сложных пространственных систем принципиально возможны и к каким следствиям они могут привести.

Как уже упоминалось, наши возможности восприятия окружающего мира ограничиваются пределом осознаваемой мерности. Граница этого предела определяется нашей способностью воспринимать и перерабатывать информацию. Чем выше уровень мерности, тем больший объем информации она несет. Этот объем можно оценить по количеству элементарных сигналов, которые содержит система при одинаковом количестве шагов квантования по каждой координатной оси и возможного числа сочетаний этих сигналов в двоичном коде. При двух шагах квантования эти показатели будут следующими (табл. 1).