БСЭ - Большая Советская энциклопедия (ДЕ)

Лит.: Салищев К. А., Основы картоведения, М., 1948.

Дели'ль(Delisle) Жозеф Никола' (4.4.1688, Париж, — 11.9.1768, там же), французский астроном и картограф, член Парижской АН (1714). Брат Г. Делиля . В 1726—47 член Петербургской АН и директор Астрономической обсерватории в Петербурге, где вёл систематические наблюдения. В 1737 измерил базисную линию в 21,5 км (по льду Финского залива) между Петергофом и Дубками (близ Сестрорецка). В 1739—40 заведовал географическим департаментом Петербургской АН. Предъявляя к картографическим материалам русских геодезистов чрезмерные требования, Д. необоснованно затянул составление «Атласа Российского», который был издан АН в 1745 после отстранения Д. от руководства географическим департаментом. Д. тайно отправил во Францию большое количество подлинников и копий карт России, часть которых опубликовал позже без согласия Петербургской АН, за что был лишён пенсии, назначенной ему после ухода из академии в 1747.

Соч.: Mémoires pour servir à l'histoire de I'astronomiе, de la géographie et de la physique, St.-Pétersbourg, 1738.

Лит.: Гнучева В. Ф., Географический департамент Академии наук 18 века, М. — Л., 1946.

Делимита'ция грани'ц(от лат. delimitatio — установление границ), в международном праве определение положения и направления государственной границы по соглашению между сопредельными государствами. Фиксируется в соответствующих договорах, которые обычно содержат довольно подробное описание прохождения линии границы на местности, а также могут отсылать к др. документам о Д. г. В соответствии с определённым в договоре положением линии границы она наносится на географическую карту, которая, как правило, является составной частью договора о Д. г. и в этом качестве служит наглядным свидетельством о положении линии границы.

Дели'мость,способность одного числа делиться на другое. Свойства Д. зависят от того, какие совокупности чисел рассматривают. Если рассматривают только целые положительные числа, то говорят, что одно число делится на другое, или, иначе, одно является кратным другого, если частное от деления первого числа (делимого) на второе (делитель) будет также целым числом. Число называется простым, если у него нет делителей, отличных от него самого и от единицы (таковы, например, числа 2,3,5,7,97,199 и т.д.), и составным в противном случае. Любое целое число можно разложить в произведение простых, например 924 = 2×2×3×7×11, причём это разложение единственно с точностью до порядка множителей (как говорят, однозначно); так, разложение числа 924 на множители может быть записано также следующим образом:

924 = 11×7×3×2×2 = 11×3×2×2×7 и т.д.,

однако все эти разложения отличаются только порядком множителей. Данное число n делится на простое число р в том и только в том случае, если р встречается среди простых множителей, на которые разлагается n . Установлен ряд признаков Д., по которым можно легко определить, делится ли число n (записанное по десятичной системе счисления) на данное простое число р . Среди этих признаков практически наиболее удобны следующие: для Д. на 2 надо, чтобы последняя цифра числа делилась на 2; для Д. на 3, — чтобы сумма цифр числа делилась на 3; для Д. на 5, — чтобы последняя цифра была 0 или 5; для Д. на 11, — чтобы разность суммы цифр, стоящих на чётных местах, и суммы цифр, стоящих на нечётных местах, делилась на 11. Имеются также признаки Д. на составные числа: для Д. на 4 надо, чтобы число, записываемое двумя последними цифрами, делилось на 4; для Д. на 8, — чтобы число, записываемое тремя последними цифрами, делилось на 8; для Д. на 9, — чтобы сумма цифр числа делилась на 9. Менее удобны признаки Д. на 7 и 13: на эти числа должна делиться разность числа тысяч и числа, выражаемого последними тремя цифрами; эта операция уменьшает число знаков в числе, и последовательное её применение приводит к трёхзначному числу, например 825 678 делится на 7, т.к. 825-678 = 147 делится на 7.

Для двух чисел а и b среди всех их общих делителей существует наибольший, называемый наибольшим общим делителем. Если наибольший общий делитель двух чисел равен единице, то числа называются взаимно простыми. Целое число, делясь на два взаимно простых числа, делится и на их произведение. На этом факте основаны простые признаки Д. на 6 = 2×3, на 10 = 2×5, на 12 = 3×4, на 15 = 3×5 и т.д.

Аналогично теории Д. целых чисел строится теория Д. для многочленов и целых алгебраических чисел. При разложении многочленов роль простых чисел играют неприводимые многочлены . Свойство быть неприводимым зависит от того, какие числа допускаются в качестве коэффициентов. При действительных коэффициентах неприводимыми могут быть многочлены только 1-й и 2-й степени, при комплексных — только 1-й степени. Однозначность будет опять условная: с точностью до числового множителя. Для целых алгебраических чисел теорема об однозначности разложения на множители будет неверна; так, среди чисел вида

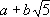
( а и b — целые) число 4 (для которого а = 4, b = 0) допускает два разложения:

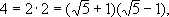
причём ни один из множителей дальше не разложим. Это обстоятельство привело к введению так называемых идеальных чисел, или идеалов , для которых уже все теоремы о разложении сохраняются.

Лит.: Воробьев Н. Н., Признаки делимости, М., 1963.

Делинкве'нт(от лат. delinquens, родительный падеж delinquentis — совершающий проступок), в англо-американском праве лицо, не выполнившее лежащей на нём в силу закона или договора обязанности, допустившее какое-либо нарушение, совершившее преступление и т.п. — отсюда термины: делинквентность (нарушение или преступление), делинквентный (невыполненная обязанность, например неуплаченный вовремя налог). В английском законодательстве и административно-судебной практике Д. именуются несовершеннолетние, поведение которых обусловливает необходимость применения различных мер исправительного воздействия, предусмотренных уголовным законодательством или специальным законодательством о молодёжи (в том числе помещение в закрытые воспитательные учреждения).

Б. С. Никифоров.

Дели'нья,река в Якутской АССР, правый приток р. Томпо (бассейн р. Алдан). Длина 357 км , площадь бассейна 12 500 км 2 . Берёт начало на Эльгинском плоскогорье, течёт среди гор на З., затем на Ю. В верховьях протекает через одноимённое озеро. Питание снеговое и дождевое. Приток справа — Нолучу.