БСЭ - Большая Советская энциклопедия (Пр)

Преде'л,одно из основных понятий математики. П. — постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой последовательности, с помощью которого могут быть определены понятия П. функции, П. последовательности точек пространства, П. интегральных сумм.

Предел последовательности.Пусть задана последовательность действительных чисел x n, n = 1 , 2,... Число а называется пределом этой последовательности, если для любого числа e > 0 существует такой номер n e, что для всех номеров n ³ n e выполняется неравенство | x n— a | < e. В этом случае пишется

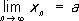
(lim — первые буквы латинского слова limes), или

x n® a при n ® ¥.

Если последовательность имеет П., то говорят, что она сходится. Так, последовательность 1/ n, n = 1, 2,..., сходится и имеет своим П. число 0. Не всякая последовательность имеет П., например последовательность 1, —1, 1,..., (—1) n+1,... не имеет П. Последовательность, не имеющая П., называется расходящейся. На геометрическом языке существование у последовательности П., равного а, означает, что каждая окрестность точки а содержит все члены данной последовательности, за исключением, быть может, их конечного числа.

Для П. последовательностей имеют место формулы

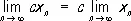( c - постоянная)

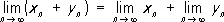
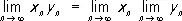
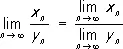
Эти формулы справедливы в предположении, что П., стоящие в их правых частях, существуют, причём в формуле для П. частного x n / y n надо ещё дополнительно потребовать, чтобы 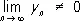. Если x n £ y n и последовательности x n и y n, n = 1, 2,... сходятся, то

т. е. при предельных переходах нестрогие неравенства сохраняются (но из x n < y n не вытекает 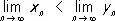, например, 1/ n > 0, n = 1, 2,... однако 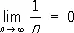). Если 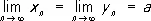и x n £ z n £ y n, то последовательность z n, n = 1, 2, ..., сходится к тому же П.:

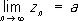
Последовательность a n, n = 1, 2,..., сходящаяся к нулю, называется бесконечно малой. Последовательность сходится к какому-либо числу тогда и только тогда, когда разность между членами последовательности и этим числом является бесконечно малой последовательностью (т. о., общее понятие П. последовательности сводится к понятию бесконечно малой ) . Так, например, последовательность 1/ 2, 2/ 3, 3/ 4, ..., n /( n + 1),... имеет своим П. единицу, поскольку разность 1 — n /( n + 1) = 1/( n + 1), n = 1, 2,... является бесконечно малой последовательностью.

Всякая возрастающая (убывающая) последовательность, ограниченная сверху (соответственно снизу), сходится. Например, если для заданного числа а обозначить через a nприближённое значение его корня 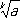( k — натуральное число) с n десятичными знаками после запятой, вычисленное с недостатком, то a n £ a n+1 £ 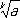, n = 1, 2, …, поэтому последовательность a n, сходится, причём из неравенства 0 £ 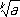- a n £ 10 -nследует, что 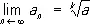. Др. примером возрастающей ограниченной сверху последовательности является последовательность длин периметров правильных многоугольников, вписанных в данную окружность, к длине которой сходится эта последовательность.

Для того чтобы сходилась произвольная последовательность x n, необходимо и достаточно, чтобы она удовлетворяла критерию Коши: для любого числа e > 0 существует такой номер N e , что для всех номеров m ³ N e и n ³ N e выполняется неравенство | x n— x m | < e.

Если последовательность x n, n = 1, 2,..., такова, что для числа e > 0 существует такой номер n e, что для всех номеров n ³ n e выполняется неравенство | x n | > e , то последовательность x n , называется бесконечно большой и пишется

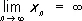
Если же при этом для любого e > 0 существует такой номер n e, что x n > e (соответственно x n < -e) для всех n ³ n e, то пишется 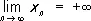(соответственно )

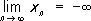Эти П. называются бесконечными. Например, 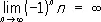. В случае же последовательности n 2, n = 1, 2, …,, можно написать не только 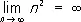но и более точное равенство 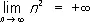. Само собой разумеется, что бесконечно большие последовательности не являются сходящимися в смысле данного выше определения этого понятия. На бесконечные П. переносятся далеко не все свойства конечных П. Например, последовательности x n= n и y n = 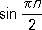— n бесконечно большие, а последовательность x n + y n,, n = 1, 2,..., ограниченная и к тому же расходящаяся.

Частичные пределы. Верхний и нижний пределы. П. (конечный и бесконечный) какой-либо подпоследовательности называется частичным пределом последней. Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность (теорема Больцано — Вейерштрасса), а из всякой неограниченной — бесконечно большую. В множестве всех частичных П. последовательности всегда имеется как наибольший, так и наименьший (конечный или бесконечный). Наибольший (соответственно наименьший) частичный П. последовательности x n, n = 1, 2,..., называют её верхним (соответственно нижним) пределом и обозначается 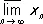(соответственно 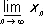) . Например,