БСЭ - Большая Советская энциклопедия (На)

Лит.: Цейтлин А. Г., Становление реализма в русской литературе, М., 1965; Кулешов В. И., Натуральная школа в русской литературе XIX в., М., 1965; Манн Ю. В., Философия и поэтика «натуральной школы», в кн.: Проблемы типологии русского реализма, М., 1969.

В. И. Кулешов.

Натура'льное исчисле'ние,исчисление естественного вывода, натуральная дедукция, общее название логических исчислений, введённых и изученных в 1934 немецким логиком Г. Генценом (и независимо польским логиком С. Яськовским) с целью формализации процесса логического вывода, как можно более точно воспроизводящей структуру обычных содержательных рассуждений, а также для решения ряда важных задач метаматематики (в том числе для доказательства непротиворечивости арифметики натуральных чисел). Основным объектом Н. и. можно считать отношение (формальной) выводимости, обозначаемое символом , обладающее, по определению, свойством А 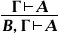(разрешение усилить посылки), 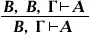(разрешение опускать одну из совпадающих посылок), 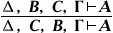(разрешение переставлять посылки). В различных формулировках Н. и. вид и число структурных правил различны; например, понимая под Д и Г не последовательности, а просто конечные множества (неупорядоченные) формул, можно обойтись без правил перестановки посылок; обычное соглашение, что каждый элемент входит в него лишь один раз, делает ненужным правило сокращения повторяющихся посылок, и т.п. Кроме того, в Н. и. входят логические правила вывода, регламентирующие процедуру введения и удаления (устранения, исключения) символов логических операций и описывающие (как и аксиомы «обычных» логических исчислений; см., например, Логика высказываний ) свойства этих операций. Вот правила классического Н. и. высказываний:

Введение

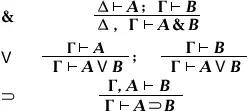
(так называемая «теорема о дедукции», см. Дедукция )

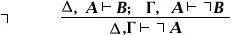
(reductio ad absurdum, или приведение к нелепости, см. Доказательство от противного ) Удаление

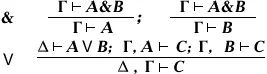
(так называемое доказательство разбором случаев)

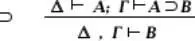
(modus ponens, или схема заключения)

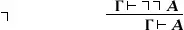
(так называемый закон снятия двойного отрицания). (В скобках указана интерпретация некоторых правил в терминах традиционной логики; интерпретация остальных правил — та же, что у соответствующих аксиом обычного исчисления высказываний, перефразировками которых они являются.) Добавление к этому списку соответствующих правил введения и удаления для кванторов приводит к Н. и. предикатов. Замена правила 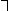-удаления на так называемое правило слабого 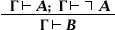(«из противоречия следует любое высказывание», см. Противоречия принцип ) приводит к интуиционистскому (конструктивному) Н. и. высказываний (а с подходящими изменениями в кванторных правилах — к интуиционистскому Н. и. предикатов; см. Математический интуиционизм , Конструктивное направление ).

Доказательство в Н. и. — это, как обычно, вывод из пустого множества посылок. В формулировках Н. и., подобных приведённой, в которых нет аксиом (кроме, быть может, А А), источником получения «логических законов», выражаемых формулами, доказуемыми без привлечения каких бы то ни было гипотез (посылок), оказывается правило É-введения. Гибкость аппарата Н. и., близость его к привычным формам содержательных рассуждений и простота получающихся выводов делают его удобным орудием логико-математического исследования. Н. и. полезно и в тех случаях, когда применяются другие системы логики: в качестве источника выводимых (дополнительных) правил вывода, применение которых также значительно упрощает логический аппарат, а также для получения эвристических (предварительных, подлежащих дальнейшему обоснованию) доводов, которые так или иначе должны предшествовать любому формальному доказательству (как источник доказываемых или опровергаемых гипотез).

Лит.: Клини С. К., Введение в метаматематику, пер. с англ., М., 1957, §§ 20, 23; Генцен Г., Исследования логических выводов, пер. с. нем., в кн.: Математическая теория логического вывода, М., 1967; Карри Х. Б., Основания математической логики, пер. с англ., М., 1969. См. также лит. при ст. Правило вывода .

Ю. А. Гастов.

Натура'льное обяза'тельство,см. в ст. Обязательство .

Натура'льное хозя'йство,тип хозяйства, при котором производство направлено на удовлетворение собственных потребностей производителя. «При натуральном хозяйстве общество состояло из массы однородных хозяйственных единиц... и каждая такая единица производила все виды хозяйственных работ, начиная от добывания разных видов сырья и кончая окончательной подготовкой их к потреблению» (Ленин В. И., Полное собрание соч., 5 изд., т. 3, с. 21—22). Н. х. возникло в глубокой древности и господствовало на стадии, когда ещё не было общественного разделения труда, обмена и частной собственности. В рабовладельческом обществе и при феодализме Н. х. оставалось господствующим, несмотря на развитие обмена и товарно-денежных отношений. К. Маркс указывал, что Н. х. преобладает на базисе всякой системы личной зависимости, как рабской, так и крепостнической (см. К. Маркс и Ф. Энгельс, Соч., 2 изд., т. 24, с. 544). Для Н. х. характерны замкнутость, ограниченность, традиционность и разобщённость производства, рутинная техника и медленные темпы развития. С углублением общественного разделения труда Н. х. постепенно вытесняется товарным производством. При капитализме в крестьянских хозяйствах сохраняются черты и пережитки Н. х. В переходный период от капитализма к социализму в некоторых странах Н. х. сохраняется как один из экономических укладов. Среди существовавших в России сразу после Октябрьской революции 1917 общественно-экономических укладов В. И. Ленин называл «... патриархальное, т. е. в значительной степени натуральное, крестьянское хозяйство» (Полное собрание соч., 5 изд., т. 36, с. 296).