БСЭ - Большая Советская энциклопедия (На)
- Название:Большая Советская энциклопедия (На)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ - Большая Советская энциклопедия (На) краткое содержание
Большая Советская энциклопедия (На) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
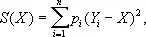
где p i = k/ s i 2и s i 2= Dd i = Ed i 2
(коэффициент k > 0 можно выбирать произвольно). Величину p i называют весом, a s i — квадратичным отклонением измерения с номером i . В частности, если все измерения равноточны, то s 1= s 2=... = s n , и в этом случае можно положить p 1= p 2=... = p n = 1; если же каждое Y i , — арифметическое среднее из n i , равноточных измерений, то полагают p i = n i .
Сумма S ( X ) будет наименьшей, если в качестве Х выбрать взвешенное среднее:
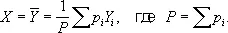
Оценка 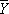 величины m лишена систематической ошибки, имеет вес Р и дисперсию
величины m лишена систематической ошибки, имеет вес Р и дисперсию
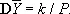
В частности, если все измерения равноточны, то Y — арифметическое среднее результатов измерений:
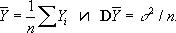
При некоторых общих предположениях можно показать, что если количество наблюдений n достаточно велико, то распределение оценки 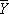 мало отличается от нормального с математическим ожиданием m и дисперсией k/P . В этом случае абсолютная погрешность приближённого равенства
мало отличается от нормального с математическим ожиданием m и дисперсией k/P . В этом случае абсолютная погрешность приближённого равенства
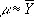
меньше
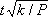
с вероятностью, близкой к значению интеграла
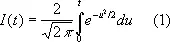
[напр., I (1,96) = 0,950; I (2,58) = 0,990; I (3,00) = 0,997].
Если веса измерений p i заданы, а множитель k до наблюдений остаётся неопределённым, то этот множитель и дисперсия оценки 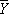 могут быть приближённо оценены по формулам:
могут быть приближённо оценены по формулам:
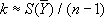
и
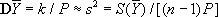
(обе оценки лишены систематических ошибок).
В том практически важном случае, когда ошибки d i подчиняются нормальному распределению, можно найти точное значение вероятности, с которой абсолютная погрешность приближённого равенства
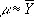
окажется меньше ts ( t — произвольное положительное число). Эту вероятность, как функцию от t , называют функцией распределения Стьюдента с n - 1 степенями свободы и вычисляют по формуле
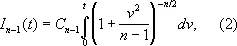
где постоянная C n -1выбрана таким образом, чтобы выполнялось условие: I n -1(¥) = 1. При больших n формулу (2) можно заменить формулой (1). Однако применение формулы (1) при небольших n привело бы к грубым ошибкам. Так, например, согласно (1), значению I = 0,99 соответствует t = 2,58; истинные значения t , определяемые при малых n как решения соответствующих уравнений l n -1( t ) = 0,99, приведены в таблице:
Пример. Для определения массы некоторого тела произведено 10 независимых равноточных взвешиваний, давших результаты Y i (в г ):
(здесь n i — число случаев, в которых наблюдался вес Y i , причём n = S n i , = 10). Так как все взвешивания равноточные, то следует положить p i = n i и в качестве оценки для неизвестного веса m, выбрать величину
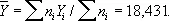
Задавая, например, I 9= 0,95, по таблицам распределения Стьюдента с девятью степенями свободы можно найти, что t = 2,262, и поэтому в качестве предельной абсолютной погрешности приближённого равенства m » 18,431 следует принять величину
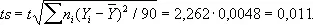
Т. о. 18,420 < m < 18,442.
Случай нескольких неизвестных (линейные связи). Пусть n результатов измерений Y 1, Y 2,..., Y n связаны с m неизвестными величинами x 1, x 2,..., х m ( m < n ) независимыми линейными отношениями
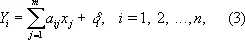
где a ij — известные коэффициенты, а d i — независимые случайные ошибки измерений. Требуется оценить неизвестные величины x j (эту задачу можно рассматривать как обобщение предыдущей, в которой m = x 1 и m = a i1 = 1; i = 1,2,..., n ).
Так как Еd i = 0, то средние значения результатов измерений y i , = E y i . связаны с неизвестными величинами x 1, x 2,..., х m линейными уравнениями (линейные связи):
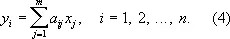
Следовательно, искомые величины x j представляют собой решение системы (4), уравнения которой предполагаются совместными. Точные значения измеряемых величин y i и случайные ошибки d i обычно неизвестны, поэтому вместо систем (3) и (4) принято записывать так называемые условные уравнения
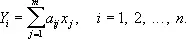
Согласно Н. к. м., качестве оценок для неизвестных x j применяют такие величины X j , для которых сумма квадратов отклонений
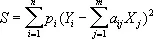
будет наименьшей (как и в предыдущем случае, p i — вес измерения Y i , — величина, обратно пропорциональная дисперсии случайной ошибки d i ). Условные уравнения, как правило, несовместны, т. е. при любых значениях X j разности
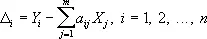
не могут, вообще говоря, все обратиться в нуль, и в этом случае
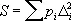
Интервал:
Закладка:










