БСЭ - Большая Советская энциклопедия (На)

также не может обратиться в нуль. Н. к. м. предписывает в качестве оценок выбрать такие значения X j , которые минимизируют сумму S . В тех исключительных случаях, когда условные уравнения совместны и, значит, обладают решением, это решение совпадает с оценками, полученными согласно Н. к. м.

Сумма квадратов S представляет собой квадратичный многочлен относительно переменных X j ; этот многочлен достигает минимума при таких значениях X 1, X 2,..., Х m , при которых обращаются в нуль все первые частные производные:

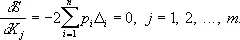
Отсюда следует, что оценки X j , полученные согласно Н. к. м., должны удовлетворять системе так называемых нормальных уравнений, которая в обозначениях, предложенных Гауссом, имеет вид:

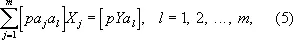
где

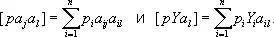
Оценки X j , получающиеся в результате решения системы нормальных уравнений, лишены систематических ошибок ( E x j = x j ); дисперсии D x j ; величин X j равны kd jj/d , где d — определитель системы (5), а d jj — минор, соответствующий диагональному элементу [ ра ja j ] (иными словами, d jj/d — вес оценки X j ). Если множитель пропорциональности k ( k называется дисперсией на единицу веса) заранее неизвестен, то для его оценки, а также для оценки дисперсии D x j служат формулы:

k » S/ ( n - m ) и D x j » s 2 j = Sd jj/d ( n - m )

( S — минимальное значение исходной суммы квадратов). При некоторых общих предположениях можно показать, что если количество наблюдений n достаточно велико, то абсолютная погрешность приближённого равенства x i » X j меньше ts j с вероятностью, близкой к значению интеграла (1). Если случайные ошибки наблюдений d i подчиняются нормальному распределению, то все отношения ( X j - x j )/ s j распределены по закону Стьюдента с n - m степенями свободы [точная оценка абсолютной погрешности приближённого равенства производится здесь с помощью интеграла (2) так же, как в случае одного неизвестного]. Кроме того, минимальное значение суммы S в вероятностном смысле не зависит от X 1, X 2,..., X m и поэтому приближённые значения дисперсий оценок D x j » s 2 j не зависят от самих оценок X j .

Один из наиболее типичных случаев применения Н. к. м. — «выравнивание» таких результатов наблюдений Y i , для которых в уравнениях (3) a ij = a j ( t i ), где a j ( t ) — известные функции некоторого параметра t (если t — время, то t 1, t 2,... — те моменты времени, в которые производились наблюдения). Особенно часто встречается в приложениях случай так называемой параболической интерполяции, когда a j ( t ) — многочлены [например, a 1( t ) = 1, a 2( t ) = t , a 3( t ) = t 2 ,... и т.д.]; если t 2— t 1= t 3— t 2=... = t n — t n -1, a наблюдения равноточные, то для вычисления оценок X j можно воспользоваться таблицами ортогональных многочленов, имеющимися во многих руководствах по современной вычислительной математике. Другой важный для приложения случай — так называемая гармоническая интерполяция, когда в качестве a j ( t ) выбирают тригонометрические функции [например, a j ( t ) = cos ( j - 1) t , j = 1, 2,..., m ].

Пример. Для оценки точности одного из методов химического анализа этим методом определялась концентрация CaO в десяти эталонных пробах заранее известного состава. Результаты равноточных наблюдений указаны в таблице ( i — номер эксперимента, t i — истинная концентрация CaO, T i — концентрация CaO. определённая в результате химического анализа, Y i = T i - t i — ошибка химического анализа):

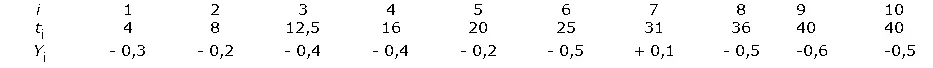
Если результаты химического анализа не имеют систематических ошибок, то E y i = 0. Если же такие ошибки имеются, то в первом приближении их можно представить в виде: E y i = a + b t i (a называется постоянной ошибкой, а b t i — методической ошибкой) или, что то же самое,

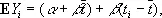
где

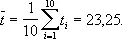
Для отыскания оценок a и b достаточно оценить коэффициенты

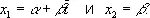
Условные уравнения в данном случае имеют вид:

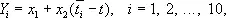
поэтому a i1 = 1, a i2 = t i - t (согласно предположению о равноточности наблюдений, все p i = 1). Так как

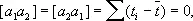
то система нормальных уравнений записывается особенно просто:

[ a 1a 1 ] X 1 = [ Ya 1 ]; [ a 2a 2 ] X 2 = [ Ya 2 ],

где

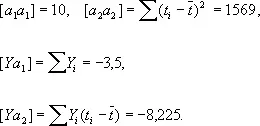
Дисперсии компонент решения этой системы суть

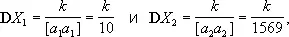
где k — неизвестная дисперсия на единицу веса (в данном случае k — дисперсия любой из величин Y i). Так как в этом примере компоненты решения принимают значения X 1= -0,35 и X 2= -0,00524, то

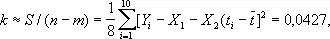
D x 1 » s 1 2 = 0,00427,

D x 2 » s 2 2 = 0,0000272,

s 1 = 0,065, s 2 = 0,00522.

Если случайные ошибки наблюдений подчиняются нормальному распределению, то отношения | X j – x j l/ s j ( j = 1, 2) распределены по закону Стьюдента. В частности, если результаты наблюдений лишены систематических ошибок, то x 1= x 2= 0 и, значит, закону Стьюдента должны подчиняться отношения | X 1|/ s 1и | X 2|/ s 2. С помощью таблиц распределения Стьюдента с n – m = 8 степенями свободы можно убедиться, что если действительно x 1= x 2= 0, то с вероятностью 0,999 каждое из этих отношений не должно превосходить 5,04 и с вероятностью 0,95 не должно превосходить 2,31. В данном случае | X 1|/ s 1= 5,38 > 5,04, поэтому гипотезу отсутствия систематических ошибок целесообразно отвергнуть; в то же время следует признать, что гипотеза об отсутствии методической ошибки ( x 2 = 0) не противоречит результатам наблюдений, так как | X 2|/ s 2= 1,004 < 2,31. Т. о., можно заключить, что для определения t по результату наблюдения Т целесообразно пользоваться приближённой формулой t = Т + 0,35.