БСЭ - Большая Советская энциклопедия (ВА)

Прямые методы. В. и. как самостоятельная научная дисциплина сформировалась в 18 в., главным образом благодаря работам Л. Эйлера .

Простейшей задачей В. и. называют задачу отыскания функции x ( t ) , доставляющей экстремум функционалу

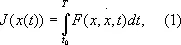
где F — непрерывная и дифференцируемая функция своих аргументов. При этом функция x ( t ) должна удовлетворять следующим условиям:

а) она должна быть кусочно дифференцируемой,

б) при t = t o и t = T она должна принимать значения

х (t o) = х 0, х (Т) = х т. (2)

Обе задачи, рассмотренные в начале статьи, являются частными случаями простейшей задачи В. и.

Первые вариационные задачи были задачами механики. Они были поставлены в 18 в. и, следуя традициям того времени, первый вопрос, на который надо было ответить, был вопрос о способе фактического отыскания функции x ( t ) , реализующей минимум функционала (1).

Эйлер создал численный метод решения задач В. и., который получил название Эйлера метода ломаных . Этот метод был первым среди большого класса, так называемых, прямых методов ; все они основаны на редукции задачи отыскания экстремума функционала к задаче отыскания экстремума функции многих переменных. Поскольку для получения решения с высокой точностью задачу приходится сводить к отысканию экстремума функции с большим числом переменных, она становится весьма сложной для ручного счёта. Поэтому долгое время прямые методы были вне основного русла, по которому направлялись усилия математиков, занимавшихся В. и.

В 20 в. интерес к прямым методам значительно усилился. Прежде всего были предложены новые способы редукции к задаче об экстремуме функции конечного числа переменных. Поясним эти идеи на простом примере. Рассмотрим снова задачу отыскания минимума функционала (1) при дополнит. условии

x (t o) = x (T) = 0 (3)

и будем разыскивать решение задачи в форме

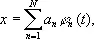
где j n(t) — некоторая система функций, удовлетворяющих условиям типа (3). Тогда функционал J (x) становится функцией коэффициентов a i:

J = J (a i,..., a N),

и задача сводится к отысканию минимума этой функции N переменных. При известных условиях, наложенных на систему функций {j n} , решение этой задачи стремится при N ® ¥ к решению задачи (1) (см. Ритца и Галёркина методы ) .

Другая причина усиления интереса к прямым методам — это систематическое изучение конечноразностных методов в задачах математической физики, начавшееся с 20-х гг. 20 в. Применение ЭВМ превращает постепенно прямые методы в основной инструмент решения вариационных задач.

Метод вариаций.Второе направление исследований — это изучение необходимых и достаточных условий, которым должна удовлетворять функция x ( t ) , реализующая экстремум функционала J (x). Его возникновение также связано с именем Эйлера. Предположим, что тем или иным способом построена функция x ( t ) . Как проверить, является ли эта функция решением задачи? Первый вариант ответа на этот вопрос был дан Эйлером в 1744. В приведённой ниже формулировке этого ответа употребляется введённое в 60-х гг. 18 в. Ж. Лагранжем понятие вариации (отсюда название — В. и.), являющееся обобщением понятия дифференциала на случай функционалов.

Пусть x ( t ) — функция, удовлетворяющая условию (2), a h (t) — произвольная гладкая функция, удовлетворяющая условию h (t o) = h (T) = 0. Тогда величина

J (x + eh) = J*(e),

где e — произвольное действительное число будет функцией e . Вариацией dJ функционала J называют производную

(dJ*/de) e= 0.

Для простейшей задачи В. и.

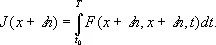
Разлагая полученное выражение в ряд по степеням e, получим

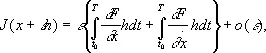
где о (e) — члены более высокого порядка. Так как h ( t o ) = h ( T ) = 0, то, проведя интегрирование по частям во втором интеграле, найдём

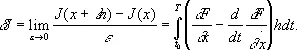
Пусть теперь x ( t ) реализует экстремум. Тогда функция J*(e) имеет экстремум при e = 0. Поэтому величина dJ должна обратиться в нуль. Отсюда следует: для того чтобы функция x ( t ) доставляла экстремум функционалу (1), необходимо, чтобы она удовлетворяла уравнению

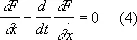
называемому уравнением Эйлера.

Это — дифференциальное уравнение 2-го порядка относительно функции x ( t ) . Необходимое условие dJ = 0 может быть применено в ряде случаев для эффективного отыскания решения вариационной задачи, поскольку функция x ( t ) необходимо должна быть решением краевой задачи x ( t o ) = x o, x ( T ) = x T для уравнения (4). Если найдено это решение и оно единственно, то найдено тем самым и решение исходной вариационной задачи. Если краевая задача допускает несколько решений, то достаточно вычислить значение функционала для каждого из решений краевой задачи и выбрать из них то, которому отвечает наименьшее значение J ( x ) . Однако указанный путь обладает одним существенным недостатком: не существует универсальных способов решения краевых задач для обыкновенных (нелинейных) дифференциальных уравнений.

Уже во 2-й половине 18 в. круг задач, изучаемых В. и., значительно расширился. Прежде всего основные результаты, относящиеся к простейшей задаче В. и., были перенесены на общий случай интегральных функционалов вида

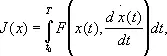
где x ( t ) — вектор-функция произвольной размерности, и на функционалы ещё более общего вида.

Условный экстремум. Задача Лагранжа.В конце 18 в. был сформулирован ряд задач на условный экстремум. Этим термином принято называть задачи отыскания функции x ( t ) , доставляющей экстремум функционалу J ( x ) при каких-либо дополнительных условиях, кроме условий на концах интервала (t 0, T). Простейшей задачей подобного вида является класс так называемых изопериметрических задач . Своим названием этот класс задач обязан следующей: среди всех замкнутых кривых данной длины найти ту, которая ограничивает максимальную площадь.