БСЭ - Большая Советская энциклопедия (ВА)

Значительно более сложной задачей является та, в которой ограничения носят характер дифференциальных уравнений. Эту задачу называют задачей Лагранжа; особое значение она приобрела в середине 20 в. в связи с созданием теории оптимального управления . Поэтому её формулировка даётся ниже на языке этой теории, возникшем после работ Л. С. Понтрягина и его учеников.

Пусть x (t) и u (t) — вектор-функции размерностей n и m соответственно, причём функция x ( t ) , которую называют фазовым вектором, при t = t o и t = T удовлетворяет граничным условиям:

x (t 0) Î e 0, x (T) Î e T (5)

где e 0и e T— некоторые множества. Простейшим примером условий типа (5) являются условия (2). Функция x ( t ) и функция u ( t ) , которую называют управлением, связаны условием

dx/dt = f (x, u, t), (6)

где f — дифференцируемая вектор-функция своих аргументов. Рассматриваемая задача состоит в следующем: определить функции x ( t ) и u ( t ) , доставляющие экстремум функционалу

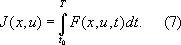
Заметим, что и простейшая задача В. и. и изопериметрическая задача являются частным случаем задачи Лагранжа.

Задача Лагранжа имеет огромное прикладное значение. Пусть, например, уравнение (6) описывает движение какого-либо динамического объекта, например космического корабля. Управление u — это вектор тяги его двигателя. Множества e 0 и e T — это две орбиты разных радиусов. Функционал (7) описывает расход горючего на выполнение маневра. Следовательно, задачу Лагранжа, применительно к данной ситуации, можно сформулировать следующим образом: определить закон изменения тяги двигателя космического аппарата, совершающего переход с орбиты e 0 на орбиту e T за заданное время так, чтобы расход топлива на этот маневр был минимальным.

Важную роль в теории подобных задач играет функция Гамильтона

H (x, y, u) = (f, y) - F.

Здесь y — вектор, называется множителем Лагранжа (или импульсом), (f, y) означает скалярное произведение векторов f и y . Необходимое условие в задаче Лагранжа формулируется следующим образом: для того чтобы функци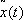и и 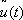были решением задачи Лагранжа, необходимо, чтобы 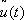была стационарной точкой функции Гамильтона Н (х, y, u), то есть, чтобы при

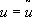
было ¶ H/ ¶ u = 0, где y — не равное тождественно нулю решение уравнения

¶y/t = —¶H/¶x = j(x, y, u, t). (8)

Эта теорема имеет важное прикладное значение, так как она открывает известные возможности для фактического нахождения векторов x ( t ) и u ( t ) .

Развитие В. и. в 19 в.Основные усилия математиков в 19 в. были направлены на исследование условий, необходимых или достаточных для того, чтобы функция x ( t ) реализовала экстремум функционала J ( x ) . уравнение Эйлера было первым из таких условий; оно аналогично необходимому условию

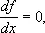
которое устанавливается в теории функций конечного числа переменных. Однако в этой теории известны ещё и другие условия. Например, для того, чтобы функция f ( x ) имела в точке минимум, необходимо, чтобы в этой точке было

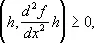
каков бы ни был произвольный вектор h. Естественно поставить вопрос: в какой степени эти результаты переносятся на случай функционалов? Для того чтобы представить себе сложность, которая здесь возникает, заметим, что функция 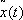может реализовать минимум среди функций одного класса и не давать минимум среди функций другого класса и т.д.

Подобные вопросы послужили источником разнообразных и глубоких исследований А. Лежандра , К. Якоби , М. В. Остроградского , У. Гамильтона , К. Вейерштрасса и многих других. Эти исследования не только обогатили математический анализ, но и сыграли большую роль в формировании идей аналитической механики и оказали серьезное влияние на развитие разнообразных отделов теоретической физики.

Развитие В. и. в 20 в.В 20 в. возник целый ряд новых направлений В. и., связанных с интенсивным развитием техники, смежных вопросов математики и вычислительной техники. Одно из основных направлений развития В. и. в 20 в. — рассмотрение неклассических задач В. и., приведшее к открытию принципа максимума Л. С. Понтрягина.

Рассмотрим снова задачу Лагранжа: определить минимум функционала

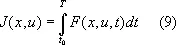
при условии

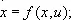
фазовый вектор x ( t ) должен удовлетворять ещё некоторым граничным условиям.

В своей классической постановке условия задачи Лагранжа не предусматривают никаких ограничений на управление u ( t ) . Выше (см. раздел Условный экстремум. Задача Лагранжа) подчёркивалась тесная связь между задачей Лагранжа и задачей управления. В рассмотренном там примере u ( t ) — тяга ракетного двигателя. Эта величина подчинена ограничениям: тяга двигателя не может превосходить некоторой величины, и угол поворота вектора тяги также ограничен. В данном конкретном примере компонента u i (i = 1,2,3) вектора тяги двигателя подчинена ограничениям

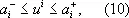
где а - i и a + i— некоторые заданные числа. Подобных примеров можно привести много.

Таким образом, в технике появилось много задач, которые сводятся к задаче Лагранжа, но при дополнительных ограничениях типа (10), записываемых в форме u Î G u, где G u — некоторое множество, которое, в частности, может быть замкнутым. Такие задачи получили название задач оптимального управления. В задаче Лагранжа можно исключить управление u ( t ) при помощи уравнения (8) и получить систему уравнений, которая содержит только фазовую переменную х и множитель Лагранжа j . Для теории оптимального управления должен был быть разработан специальный аппарат. Эти исследования привели к открытию принципа максимума Л. С. Понтрягина. Он может быть сформулирован в форме следующей теоремы: для того чтобы функци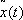и и 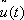были решением задачи оптимального управления чтобы они доставляли минимум функционалу (9)], необходимо, чтобы u ( t ) доставляла максимум функции Гамильтона