БСЭ - Большая Советская энциклопедия (ФР)
- Название:Большая Советская энциклопедия (ФР)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ - Большая Советская энциклопедия (ФР) краткое содержание
Большая Советская энциклопедия (ФР) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Френеля дифракция
Френе'ля дифра'кция,дифракция сферической световой волны на неоднородности (например, отверстии), размер которой сравним с диаметром одной из зон Френеля . Название дано в честь изучившего этот вид дифракции О. Ж. Френеля . Подробнее см. в ст. Дифракция света .
Френеля зеркала
Френе'ля зеркала',бизеркала Френеля, оптическое устройство, предложенное в 1816 О. Ж. Френелем для наблюдения явления интерференции когерентных световых пучков. Устройство состоит из двух плоских зеркал I и II , образующих двугранный угол, отличающийся от 180° всего на несколько угловых мин (см. рис. 1 в ст. Интерференция света ). При освещении зеркал от источника S отражённые от зеркал пучки лучей можно рассматривать как исходящие из когерентных источников S 1 и S 2 , являющихся мнимыми изображениями S . В пространстве, где пучки перекрываются, возникает интерференция. Если источник S линеен (щель) и параллелен ребру Ф. з., то при освещении монохроматическим светом интерференционная картина в виде параллельных щели равностоящих тёмных и светлых полос наблюдается на экране М , который может быть установлен в любом месте в области перекрытия пучков. По расстоянию между полосами можно определить длину волны света. Опыты, проведённые с Ф. з., явились одним из решающих доказательств волновой природы света.
Лит.: Захарьевский А. Н., Интерферометры, М., 1952; Нагибина И. М., Интерференция и дифракция света, Л., 1974.
Френеля интегралы
Френе'ля интегра'лы,интегралы вида
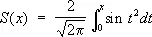
и
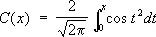
введённые О. Ж. Френелем при решении задач дифракции света . Несобственные Ф. и. равны S (¥) = С (¥) = 1/ 2. Таблицы Ф. и. приводятся во многих справочниках (например, Янке Е., Эмде Ф., Лёш Ф., Специальные функции, перевод с немецкого, 2 изд., 1968).
Френеля линза
Френе'ля ли'нза,сложная составная линза, применяемая в маячных и сигнальных фонарях. Предложена О. Ж. Френелем . Состоит не из цельного шлифованного куска стекла со сферическими или иными поверхностями, как обычные линзы, а из отдельных примыкающих друг к другу концентрических колец небольшой толщины, которые в сечении имеют форму призм специального профиля ( рис. ). Эта конструкция обеспечивает малость толщины (а следовательно, и массы) Ф. л. даже при большом угле охвата. Сечения колец таковы, что сферическая аберрация Ф. л. невелика, и лучи света от точечного источника S , помещенного в фокусе Ф. л., после преломления в кольцах выходят практически параллельным пучком (в кольцевых Ф. л.).
Ф. л. бывают кольцевыми и поясными. Первые представляют собой систему, получаемую вращением изображенного на рис . профиля вокруг оптической оси SO ; они направляют световой поток в каком-либо одном направлении. Поясные Ф. л. получают вращением этого же профиля вокруг оси ASA' , перпендикулярной SO ; они посылают свет от источника по всем горизонтальным направлениям. Диаметр Ф. л. — от 10—20 см до нескольких м .
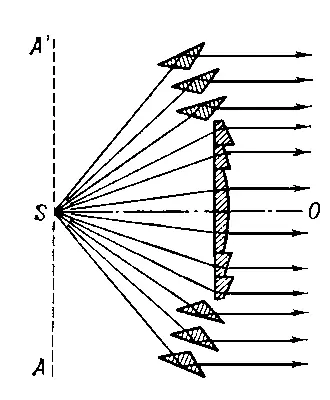
Сечение кольцевой линзы Френеля. В центе линзы — кольца, наружные поверхности к-рых являются частями тороидальных поверхностей. По краям линзы — кольца, где, помимо преломления, происходит полное внутреннее отражение.
Френеля формулы
Френе'ля фо'рмулыопределяют отношения амплитуды, фазы и состояния поляризации отражённой и преломленной световых волн, возникающих при прохождении света через неподвижную границу раздела двух прозрачных диэлектриков, к соответствующим характеристикам падающей волны. Установлены О. Ж. Френелем в 1823 на основе представлений об упругих поперечных колебаниях эфира . Однако те же самые соотношения — Ф. ф. следуют в результате строгого вывода из электромагнитной теории света при решении Максвелла уравнений и отождествлении световых колебаний с колебаниями вектора напряжённости электрического поля в световой волне, с которыми связано большинство эффектов волновой оптики.
Пусть плоская световая волна падает на границу раздела двух сред с преломления показателями n 1 и n 2 . Углы j, j'' и j"' есть соответственно углы падения, отражения и преломления, причём всегда n 1 sinj = n 2 sinj"' (закон преломления) и ½j½ = ½j'½ (закон отражения). Электрический вектор падающей волны разложим на составляющую с амплитудой А р , параллельную плоскости падения, и составляющую с амплитудой A s , перпендикулярную плоскости падения. Аналогично разложим амплитуды отражённой волны на составляющие R p и R s , а преломленной волны — на D p и D s . Ф. ф. для этих амплитуд имеют вид:
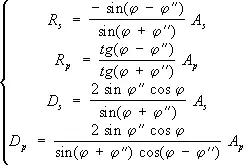 (1)
(1)
Из (1) следует, что при любом значении углов j и j"' знаки A p и D p , а также знаки A s и D s совпадают. Это означает, что совпадают и фазы, т. е. во всех случаях преломленная волна сохраняет фазу падающей. Для компонент отражённой волны ( R p и R s ) фазовые соотношения зависят от j, n 1 и n 2 . Так, если j = 0, то при n 2 > n 1 фаза отражённой волны сдвигается на p.
В экспериментах обычно измеряют не амплитуду световой волны, а её интенсивность, т. е. переносимый ею поток энергии, пропорциональный квадрату амплитуды (см. Пойнтинга вектор ). Отношения средних за период потоков энергии в отражённой и преломленной волнах к среднему потоку энергии в падающей волне называется коэффициентом отражения r и коэффициентом прохождения d . Из (1) получим Ф. ф., определяющие коэффициент отражения и прохождения для S - и р -составляющих падающей волны:
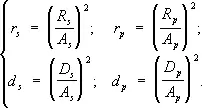 (2)
(2)
При отсутствии поглощения света r s + d s = 1 и r p + d p = 1, в соответствии с законом сохранения энергии. Если на границу раздела падает естественный свет (см. Поляризация света ), т. е. все направления колебаний электрического вектора равновероятны, то половина энергии волны приходится на р -колебания, а вторая половина — на S -колебания; полный коэффициент отражения в этом случае:
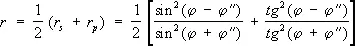 .
.
Интервал:
Закладка:










