БСЭ - Большая Советская энциклопедия (РЕ)

где величины e i характеризуют ошибки, независимые при различных измерениях и одинаково распределённые с нулевым средним и постоянной дисперсией s 2 . Случай неконтролируемой переменной х отличается тем, что результаты наблюдений ( x i , y i ), ..., ( x n , y n ) представляют собой выборку из некоторой двумерной совокупности. И в том, и в другом случае Р. а. производится одним и тем же способом, однако интерпретация результатов существенно различается (если обе исследуемые величины случайны, то связь между ними изучается методами корреляционного анализа ).

Предварительное представление о форме графика зависимости g ( x ) от х можно получить по расположению на диаграмме рассеяния (называемой также корреляционным полем, если обе переменные случайные) точек ( x i , ( x i )), где 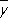( x i ) — средние арифметические тех значений у , которые соответствуют фиксированному значению x i. Например, если расположение этих точек близко к прямолинейному, то допустимо использовать в качестве приближения линейную регрессию. Стандартный метод оценки линии регрессии основан на использовании полиномиальной модели ( m ³ 1)

y ( x , b) = b 0+ b 1 x + ... + b m x m

(этот выбор отчасти объясняется тем, что всякую непрерывную на некотором отрезке функцию можно приблизить полиномом с любой наперёд заданной степенью точности). Оценка неизвестных коэффициентов регрессии b 0, ..., b mи неизвестной дисперсии s 2осуществляется наименьших квадратов методом. Оценки параметров b 0, ..., b m, полученные этим методом, называются выборочными коэффициентами регрессии, а уравнение

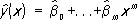
определяет т. н. эмпирическую линию регрессии. Этот метод в предположении нормальной распределённости результатов наблюдений приводит к оценкам для b 0, ..., b mи s 2, совпадающим с оценками наибольшего правдоподобия (см. Максимального правдоподобия метод ). Оценки, полученные этим методом, оказываются в некотором смысле наилучшими и в случае отклонения от нормальности. Так, если проверяется гипотеза о линейной регрессии, то

, ,

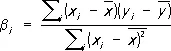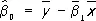где 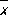и 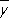— средние арифметические значений x i и y i , и оценка 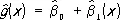будет несмещенной для g ( х ) , а её дисперсия будет меньше, чем дисперсия любой другой линейной оценки. При допущении, что величины y i нормально распределены, наиболее эффективно осуществляется проверка точности построенной эмпирической регрессионной зависимости и проверка гипотез о параметрах регрессионной модели. В этом случае построение доверительных интервалов для истинных коэффициентов регрессии b 0, ..., b mи проверка гипотезы об отсутствии регрессионной связи b i = 0, i = 1, ..., m ) производится с помощью Стьюдента распределения.

В более общей ситуации результаты наблюдений y 1, ..., y n рассматриваются как независимые случайные величины с одинаковыми дисперсиями и математическими ожиданиями

Ey i , = b 1 x 1 i + ... + b kx ki , i = 1, ..., n ,

где значения x ji , j = 1, ..., k предполагаются известными. Эта форма линейной модели регрессии является общей в том смысле, что к ней сводятся модели более высоких порядков по переменным x 1, ..., x k . Кроме того, некоторые нелинейные относительно параметров b i ; модели подходящим преобразованием также сводятся к указанной линейной форме.

Р. а. является одним из наиболее распространённых методов обработки результатов наблюдений при изучении зависимостей в физике, биологии, экономике, технике и др. областях. На модели Р. а. основаны такие разделы математической статистики, как дисперсионный анализ и планирование эксперимента ; модели Р. а. широко используются в статистическом анализе многомерном.

Лит.: Юл Дж. Э., Кендэл М. Дж., Теория статистики, пер. с англ., 14 изд., М., 1960; Смирнов Н. В., Дунин-Барковский И. В., Курс теории вероятностей и математической статистики для технических приложений, 3 изд., М., 1969; Айвазян С. А., Статистическое исследование зависимостей, М., 1968; Рао С. Р., Линейные статистические методы и их применения, пер. с англ., М., 1968. См. также лит. при ст. Регрессия .

А. В. Прохоров.

Регре'ссияв теории вероятностей и математической статистике, зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. В отличие от чисто функциональной зависимости у = f ( х ), когда каждому значению независимой переменной х соответствует одно определённое значение величины у , при регрессионной связи одному и тому же значению х могут соответствовать в зависимости от случая различные значения величины у. Если при каждом значении х = x i наблюдается n i , значений y i 1, ..., 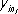величины у , то зависимость средних арифметических 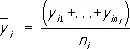от x i и является Р. в статистическом понимании этого термина. Примером такого рода зависимости служит, в частности, зависимость средних диаметров сосен от их высот; см. табл. в ст. Корреляция .

Изучение Р. в теории вероятностей основано на том, что случайные величины Х и Y , имеющие совместное распределение вероятностей, связаны вероятностной зависимостью: при каждом фиксированном значении Х = х величина Y является случайной величиной с определённым (зависящим от значения х ) условным распределением вероятностей. Р. величины Y по величине Х определяется условным математическим ожиданием Y , вычисленным при условии, что Х = х :

Е( Y ê х ) = u ( х ).

Уравнение у = u ( х ), в котором х играет роль «независимой» переменной, называется уравнением регрессии, а соответствующий график — линией регрессии величины Y по X. Точность, с которой уравнение Р. Y по Х отражает изменение Y в среднем при изменении х, измеряется условной дисперсией величины Y , вычисленной для каждого значения Х = х :