БСЭ - Большая Советская энциклопедия (РЕ)

В зависимости полных эффективных поперечных сечений рассеяния s от энергии Е Р. часто проявляются в виде колоколообразного (т. н. брейт-вигнеровского) максимума:

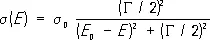(1)

(форма которого совпадает, например, с зависимостью квадрата амплитуды колебаний от частоты w в механической системе при изменении w в окрестности резонансной частоты). Энергия Е, соответствующая максимуму сечения s = s 0 , сопоставляется с массой Р. М (по формуле относительности теории М = E 0/ c 2 . В физике элементарных частиц массу принято выражать в энергетических единицах, т. е. считать с = 1; тогда М = E 0) . Величина Г является полной шириной максимума в энергетической шкале.

Первый Р. был открыт в начале 50-х гг. Э. Ферми с сотрудниками при изучении процесса взаимодействия p +мезонов с протонами на протонном циклотроне в Чикаго (США). Этот Р. —D 3, 3в современных обозначениях (первая цифра индекса у символа Р. означает удвоенный изотопический спин I частицы, вторая — её удвоенный спин J ) — можно представлять себе как возбуждённое состояние нуклона (N), в которое последний переходит, поглотив p-мезон (пион). Собственная масса Р. D 3, 3, равная полной энергии системы N + p в системе центра инерции (с. ц. и. ) этих частиц, М = (1233 ± 3) Мэв , а время жизни t = 5,7×10 -24 сек. Величина, обратная t, определяет вероятность распада частицы. Вместо времени жизни в физике Р. чаще используют полную энергетическую ширину G, которая связана с t соотношением t 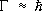, (вытекающим из неопределённостей соотношения для энергии и времени). Р. D 3, 3имеет полную ширину Г = (116 ± 6) Мэв , спин J = 3/ 2и изотопический спин I = 3/ 2.

В квантовомеханической амплитуде T 3, 3( E ) pN-pacceяния в состоянии с I = J = 3/ 2этот Р. проявляется в виде т. н. брейт-вигнеровского вклада

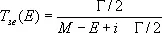, (2)

квадрат модуля которого пропорционален выражению (1). Здесь Е — полная энергия системы pN в с. ц. и. Распадается D 3, 3только на p-мезон и нуклон. Т. о., реакции образования и распада D 3, 3взаимно-обратны: p + N Û D 3, 3. Р., обладающие этим свойством, называются упругими. Р., которые могут распадаться двумя и более способами (каналами), называются неупругими. Большое количество Р. было открыто в 1-й половине 60-х гг. в экспериментах, выполненных на протонных ускорителях.

Р. делятся на 2 группы: а) барионные резонансы, обладающие барионным зарядом ( В = 1) и распадающиеся на мезоны и один стабильный барион ; б) мезонные (или бозонные) резонансы, распадающиеся на мезоны ( В = 0). Р. с ненулевой странностью называемые странными Р.

Основные методы обнаружения Р. таковы. а) Максимум в полном эффективном сечении рассеяния. В полном эффективном сечении наблюдается колоколообразный максимум s( E ) ~ êТ БВ( Е )ï 2, положение и полная ширина которого в шкале Е равны М и Г соответственно. Этот метод, однако, не позволяет провести полного определения квантовых чисел Р., в частности спина.

б) Фазовый анализ. Здесь исходными измеряемыми величинами являются дифференциальные сечения упругого рассеяния, т. е. сечения, измеряемые как функции угла рассеяния J и полной энергии Е. Квантовомеханическая амплитуда рассеяния T (J, Е ) затем разлагается в ряд по сферическим функциям , а в простейшем бесспиновом случае — по полиномам Лежандра P l (cos J):

T (J, E ) = 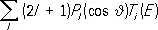(3)

Коэффициенты T l ( E ) этого разложения — парциальные волны рассеяния с орбитальным (угловым) моментом, равным целому положительному числу l — определяются из экспериментальных данных как комплексные функции действительного переменного Е. Р. со спином J = l проявляется в виде брейт-вигнеровского вклада (2) в T l ( E ). Этот метод позволяет определять все характеристики Р. (массу, ширину, спин, чётность и т. д. ).

Методы а) и б) используются в основном для обнаружения барионных Р.

в) Метод максимумов в массовых распределениях используется при обработке данных по неупругим реакциям вида а + b ® c 1+ c 2+ ... + c n , когда в результате соударения двух частиц а и b возникает n частиц ( n ³ 3). Здесь строят распределения числа событий с двумя (или несколькими) выделенными в конечном состоянии частицами, например c 1, c 2, в зависимости от суммарной энергии этих частиц в их с. ц. и.; в этой системе суммарная энергия E 12= E 1+ E 2определяет т. н. «эффективную массу» M 12пары частиц c 1+ c 2 . Распределение по M 12называется массовым распределением. Максимум в массовом распределении около среднего значения M 12= М* интерпретируется как Р. с массой М* , который может распадаться на частицы c 1и c 2. Данный метод можно успешно применять и в тех случаях, когда Р. распадается на сравнительно большое число частиц.

Вариантом этого метода может считаться метод «недостающей массы». Он используется в тех случаях, когда, например n = 3, и регистрировать частицу c 3легче, чем частицы c 1и c 2 . Энергию пары частиц c 1, c 2вычисляют по разности E 12= Е ав — E 3(как «недостающую» энергию). Р. проявляется как максимум в распределении по «недостающей» массе. Метод массовых распределений — основной способ обнаружения мезонных Р.

До ноября 1974 было открыто более 200 Р., которые группируются примерно в 40 барионных и 25 мезонных изотопических мультиплетов (см. Изотопическая инвариантность ). Массы барионных Р. лежат в интервале от 1,2 до 3 Гэв, мезонных — от 700 до 1800 Мэв. Нижние границы массовых спектров Р. определяются массами ядерно-стабильных (т. е. стабильных относительно распадов за счёт сильного взаимодействия) мезонов и барионов, а верхние — экспериментальными возможностями их обнаружения.

В ноябре 1974 открыли 2 новых тяжёлых мезонных Р. (т. н. Y-частицы) с массами примерно 3,1 и 3,7 Гэв и необычными свойствами: несмотря на наличие мезонных распадов, частицы Y 1и Y 2обладают очень малой шириной ( ~ 90 кэв и ~0,5 Мэв ) . В январе 1975 был обнаружен ещё один мезонный Р. с массой около 4,2 Гэв.

Р., лежащие в верхней части массового спектра, обладают большими спинами и большими ширинами. Наибольший установленный спин J = 11/ 2(Р. D 3, 11с массой М = 2,4 Гэв ). Эти Р. могут распадаться многими способами. Количество возможных каналов распада быстро увеличивается с ростом энергии. В области 1,5—2 Гэв барионные Р., например, имеют около 5 различных каналов распада. Важная особенность механизма многочастичных каналов распада тяжёлых Р. — его каскадность, т. е. многоступенчатость. Так, например, нестранный барионный Р. D 3, 7( I = 3/ 2, J = 7/ 2, М = 1950 Мэв ), образующийся в pN-coyдарениях, кроме основного канала двухчастичного распада D 3, 7® p+ N, обладает др. возможностями распада среди которых доминирует распад на 2 пиона и нуклон: D 3, 7® p+ +p+ N; однако этот процесс идёт в 2 этапа: сначала D 3, 7распадается на пион и D 3,3, а затем D 3, 3распадается на p и N: