БСЭ - Большая Советская энциклопедия (РЕ)

Лит.: Хилл Р. Д., Резонансные частицы, в книге: Элементарные частицы, пер. с англ., в. 3, М., 1965, с. 68—82: Дубовиков М. С., Симонов Ю. А., Распад резонансных состояний и определение их квантовых чисел, «Успехи физических наук», 1970, т. 101, в. 4, с. 655—96; Ширков Д. В., Свойства траекторий полюсов Редже, там же, 1970, т. 102, в. 1, с. 87—104; Новожилов Ю. В., Введение в теорию элементарных частиц, М., 1972.

Д. В. Ширков.

Резона'тор,колебательная система с резко выраженными резонансными свойствами (см. Резонанс ) . На практике Р. обычно называют колебательные системы с распределёнными параметрами (с бесконечным числом степеней свободы). Р. упругих колебаний являются струны, стержни (ножки камертона), мембраны, резонаторы акустические и др. Электромагнитным Р. являются полости, ограниченные проводящими стенками (см. Объёмный резонатор ), системы зеркал (см. Открытый резонатор ), кристаллические пластинки (см. Кварцевый генератор ) и т. д.

Резона'тор акусти'ческий,резонатор Гельмгольца, сосуд, сообщающийся с внешней средой через небольшое отверстие или трубку, называемую горлом Р. а. Характерная особенность Р. а. — способность совершать низкочастотные собственные колебания , длина волны которых значительно больше размеров Р. а. Собственная частота f 0Р. а. с горлом вычисляется по формуле f 0= ( с /2p) 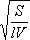, где с — скорость звука в воздухе, S и l — площадь поперечного сечения и длина трубки соответственно, V — объём сосуда. Если Р. а. поместить в гармоническое звуковое поле, частота которого равна f 0 , в нём возникают колебания с амплитудой, во много раз превышающей амплитуду звукового поля. В негармоническом звуковом поле Р. а. реагирует только на колебания с частотой, равной его собственной. Поэтому набор резонаторов с различными собственными частотами может применяться для звука анализа. Поскольку амплитуда колебательной скорости в горле резонатора на частоте f 0велика, при наличии трения в нём возникает сильное поглощение звука этой частоты. Это свойство Р. а. используется при создании т. н. резонансных звукопоглотителей в архитектурной акустике. Р. а. применяются также как элементы резонансных отражателей для уменьшения передачи низкочастотного шума по звукопроводам, т. к. малый входной импеданс Р. а., помещенного на стенке звукопровода, на частоте f 0резко изменяет условия распространения волны с этой частотой. Пузыри в жидкости и воздушной полости в некоторых др. средах, например резине, также являются Р. а., поэтому наличие большого числа пузырей в воде вызывает сильное поглощение звука и т. о. препятствует распространению звуковых волн.

Теория Р. а. была разработана Г. Гельмгольцем и Дж. Рэлеем.

Резо'рбция(от лат. resorbeo — поглощаю), 1) в физиологи и повторное поглощение; то же, что всасывание ; 2) в патологии и патологической физиологии рассасывание (например, при лейкозах Р. кости идёт очень интенсивно, сопровождаясь истончением и полным рассасыванием костных балок).

Резорци'н, м -диоксибензол, бесцветные сладковатого вкуса кристаллы, хорошо растворимые в воде, спирте, эфире; t пл110,8 °С, t kип280,8 °С. Р. — один из простейших двухатомных фенолов (наряду с гидрохиноном и пирокатехином ). В промышленности его обычно получают щелочным плавлением м -бензолдисульфокислоты. Р. применяют в производстве резорцино-альдегидных смол (см. Феноло-альдегидные смолы ), азокрасителей (например, взаимодействием с диазотированной сульфаниловой кислотой получают резорциновый жёлтый), флуоресцеина , стабилизаторов и пластификаторов высокомолекулярных соединений, взрывчатых веществ (см. Тринитрорезорцинат свинца ), лекарственных препаратов (например, антигельминтного средства — 4- н -гексилрезорцина). В аналитической химии Р. используют для колориметрического определения цинка, свинца и др. элементов, сахаров, фурфурола, лигнина, в медицине — как компонент мазей и в виде растворов при лечении кожных заболеваний.

Результа'нт(от лат. resultans, родительный падеж resultantis — отражающийся), алгебраическое выражение, применяемое при решении систем алгебраических уравнений. Р. двух многочленов f ( x ) = a 0 x n+ .. + a nи g ( x ) = b 0 x s+...+ b s(возможно, что a 0= 0 или b 0= 0) называется определитель

,

где на свободных местах стоят нули; коэффициенты a 0, a 1, ..., a nзанимают s строк, а коэффициенты b 0 b 1 , ..., b nзанимают n строк. Если a 0¹ 0 и b 0¹ 0, то

,

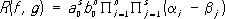где a 1, a 2, ..., a n— корни f ( x ), b 1, b 2,. .., b s— корни g ( x ). Р. равен нулю тогда и только тогда, когда f ( x ) и g ( х ) обладают общим корнем или когда их старшие коэффициенты оба равны нулю.

Пусть даны 2 уравнения Р ( х , у ) = 0 и Q ( x , y ) = 0, где Р и Q — многочлены относительно х и у. Если расположить эти многочлены по степеням х и приравнять нулю Р. получающихся многочленов, то получится уравнение относительно у степени, не превосходящей sn, где n — степень Р относительно х и у, a s — степень Q. Если x = x 0, у = y 0 — решение данной системы уравнений, то у = y 0является корнем уравнения R ( f , g ) = 0. Это позволяет свести решение системы двух уравнений к решению одного уравнения.

Р. многочлена и его производной с точностью до знака равен дискриминанту многочлена. Равенство нулю дискриминанта показывает наличие у многочлена кратных корней.

Лит.: Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971.

Ре'зус,бенгальский макак (Масаса mulatta), узконосая обезьяна рода макаков. Длина тела около 60 см , хвоста 25—30 см. Телосложение плотное, окраска шерсти тусклая, зеленовато-желтоватая. Лицо, уши и кисти розовые, седалищные мозоли красные. Живут стадами в лесах Юго-Восточной Азии, включая полуостров Индостан; встречаются в Гималаях от Непала до Северной Бирмы. Обитают на деревьях, но часто спускаются на землю. Хорошо плавают и ныряют. Р. используют как лабораторных животных для медицинских и биологических экспериментов.