БСЭ БСЭ - Большая Советская Энциклопедия (АТ)

Ядро в А. также может обладать собственным механическим моментом — ядерным спином, с которым связан небольшой ядерный магнитный момент (в сотни и тысячи раз меньший электронного магнитного момента), а в некоторых случаях и т. н. квадрупольный электрический момент (см. Моменты атомных ядер ) . Это приводит к дополнительным очень малым взаимодействиям ядра и электронов, обусловливающим дополнительное расщепление уровней энергии А. — т. н. сверхтонкую структуру (малую по сравнению с тонкой структурой).

Квантовые состояния атома водорода.Важнейшую роль в квантовой теории А. играет теория простейшего одноэлектронного А., состоящего из ядра с зарядом + Ze и электрона с зарядом — е, — теория А. водорода Н и водородоподобных ионов Не +, Li 2+, Ве 3+,... (изоэлектронного ряда, см. выше), называется обычно теорией А. водорода. Методами квантовой механики можно получить точную и полную характеристику состояний электрона в одноэлектронном А. Задача о сложных (многоэлектронных) атомах решается лишь приближённо; при этом исходят из результатов решения задачи об одноэлектронном А.

Уровни энергии А. водорода и водородоподобных ионов. Энергия одноэлектронного А. (без учёта спина электрона) равна

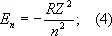
целое число n = 1, 2, 3, ... определяет возможные дискретные значения энергии — уровни энергии; его называют главным квантовым числом. R — Ридберга постоянная, равная 13,6 эв. Уровни энергии А. водорода на схеме рис. 1 , б построены для Z = 1 согласно формуле (4); они сгущаются (сходятся) к границе ионизации Е ¥= 0, соответствующей n = ¥ (уровни энергии с n > 5 на схеме не показаны). Для водородоподобных ионов изменяется (в Z 2раз) лишь масштаб энергий. Энергия ионизации водородоподобного А. (энергия связи электрона в таком А.) равна (в эв )

Е ион= E ¥ — E 1= RZ 2= 13,6Z 2 (5)

что даёт для Н, Не +, Li 2+, ... значения 13,6 эв , 54,4 эв , 122,4 эв , ...

Основная формула (4) соответствует выражению U ( r ) = —Ze 2/r для потенциальной энергии электрона, притягиваемого ядром с зарядом +Ze [см. (2) и рис. 1 , а для случая Z = 1]. Эта формула была впервые выведена Н. Бором в его теории А. (1913) путём рассмотрения движения электрона вокруг ядра по круговой орбите радиуса r . Уровням энергии (4) соответствуют орбиты радиуса

a nZ = a 0 n 2/ Z (6)

где постоянная a 0 = 0,529 10 —8 см = 0,529 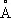— радиус первой круговой орбиты А. водорода, соответствующей его основному уровню (этим боровским радиусом часто пользуются в качестве удобной единицы для измерений длин в атомной физике). Радиус орбит пропорционален квадрату главного квантового числа n 2 и обратно пропорционален Z ; для водородоподобных ионов масштаб линейных размеров уменьшается в Z раз по сравнению с А. водорода.

Характеристика квантовых состояний атома водорода. Согласно квантовой механике, состояние А. водорода полностью определяется дискретными значениями четырёх физических величин: энергии Е, орбитального момента M l, (момента количества движения электрона относительно ядра); проекции M lz орбитального момента на направление z (выбранное произвольно в пространстве); проекции M sz спинового момента (собственного момента количества движения электрона M s ) . Возможные значения этих физических величин, в свою очередь, определяются соответствующими квантовыми числами:

1) Е — по закону (4) — главным квантовым числом n =1, 2, 3, ...;

2) М l— по закону M l 2= ( h 2/4 p 2 ) l ( l + 1) [при l " 1, M l 2= ( h 2/4 p 2 ) l 2— орбитальным (или азимутальным) квантовым числом l = 0,1, 2, ..., n— 1;

3) M lz— по закону M lz= ( h/2 p) m lz— магнитным орбитальным квантовым числом m l= l, l— 1, ..., — l ;

4) M sz— по закону M sz= ( h/2 p) m s— магнитным спиновым квантовым числом m s = 1/ 2, — 1/ 2 .

Значения квантовых чисел n, l, m l, m s и характеризуют состояние электрона в А. водорода. Энергия А. водорода зависит только от n, и уровню энергии с заданным n соответствует ряд состояний, отличающихся значениями l , m l и m s. Состояния с заданными значениями n и l принято обозначать как 1 s, 2 s, 2 p, 3 s, ..., где цифры указывают значение n, а буквы s, р, d, f (дальше по латинскому алфавиту) — соответственно значения l = 0, 1, 2, 3, ... При заданных n и l число различных состояний равно 2(2 l + 1) — числу комбинаций значений m l и m s (первое принимает 2 l + 1 значение, второе — 2 значения). Общее число различных состояний с заданными n и l при учёте, что l может принимать значения от 0 до n— 1, получается равным

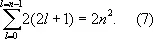
Т. о., каждому уровню энергии А. водорода соответствует 2, 8, 18, ..., 2n 2 (при n = 1, 2, 3, ...) различных стационарных квантовых состояний ( рис. 2 ). Если уровню энергии соответствует лишь одно квантовое состояние, то его называют невырожденным, если два или более — вырожденным (см. Вырождение ) , а число таких состояний g называются степенью или кратностью вырождения (для невырожденных уровней энергии g = 1). Уровни энергии А. водорода являются вырожденными, а их степень вырождения g n= 2 n 2.

Для различных состояний А. водорода получается и различное распределение электронной плотности. Оно зависит от квантовых чисел n, l и / m i / . При этом электронная плотность для s -cocтояний ( l = 0) отлична от нуля в центре, т. е. в месте нахождения ядра, и не зависит от направления (сферически симметрична), а для остальных состояний ( l > 0) она равна нулю в центре и зависит от направления. Распределение электронной плотности для состояний А. водорода с n = 1, 2 и 3 показано на рис. 3 (оно получено фотографированием специальных моделей); размеры «электронного облака» растут примерно пропорционально n 2 (масштаб на рис. 3 уменьшается при переходе от n = 1 к n = 2 и от n = 2 к n = 3) , что соответствует увеличению радиуса орбит по формуле (6) в теории Бора.

Квантовые состояния электрона в водородоподобных ионах характеризуются теми же четырьмя квантовыми числами n, l, m l и m s, что и в А. водорода. Сохраняется и распределение электронной плотности, только она увеличивается в Z раз и на рис. 3 масштабы нужно уменьшить также в Z раз. Соответственно уменьшаются и размеры орбит.