БСЭ БСЭ - Большая Советская Энциклопедия (БЕ)

Бесконе'чно больша'яв математике, переменная величина, которая в данном процессе изменения становится и остаётся по абсолютной величине больше любого наперёд заданного числа. Изучение Б. б. величин может быть сведено к изучению бесконечно малых, т.к. если у есть Б. б. величина, то обратная ей величина z = 1/ yявляется бесконечно малой. Тот факт, что переменная у является Б. б., записывают в виде lim y = ¥. При этом символ¥ («бесконечность») является просто условным обозначением того, что у есть Б. б. величина. Возможна и др. точка зрения, в силу которой ¥ является несобственным элементом, присоединяемым к множеству действительных чисел (см. Бесконечность в математике). Применительно к функции аргумента х развёрнутое определение Б. б. звучит так: функция f (x), определённая в окрестности точки х 0, называется Б. б. при х, стремящемся к х 0, если для любого числа N > 0 найдётся такое число d>0, что для всех x ¹ x 0и таких, что |х - х 0| < d , выполняется неравенство |f (x)| > N . Это свойство записывается в виде

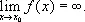
С. Б. Стечкин.

Бесконе'чно ма'лаяв математике, переменная величина, стремящаяся к пределу, равному нулю. Для того чтобы понятие Б. м. имело точный смысл, необходимо указывать тот процесс изменения, при котором данная величина становится Б. м. Например, величина y = 1/ x является Б. м. при аргументе х, стремящемся к бесконечности, а при х, стремящемся к нулю, она оказывается бесконечно большой. Если предел переменной у конечен и равен а , то lim (y - a ) = 0 и обратно. Поэтому понятие Б. м. величины можно положить в основу общего определения предела переменной величины. Теория Б. м. является одним из способов построения теории пределов.

При рассмотрении нескольких переменных величин, участвующих в одном и том же процессе изменения, переменные у и z называются эквивалентными, если lim z/y = 1; если при этом у является Б. м., то у и z называются эквивалентными Б. м. Переменная z называется Б. м. относительно у, если z/y есть Б. м. Последний факт часто записывается в виде z = о ( у ) (читается: «z есть о малое от у»). Если при этом у является Б. м., то говорят, что z есть Б. м. более высокого порядка, чем у. Часто среди нескольких Б. м., участвующих в одном и том же процессе изменения, одна из них, скажем у, принимается за главную, и с ней сравниваются все остальные. Тогда говорят, что z есть Б. м. порядка k > 0, если предел lim z/ук существует и отличен от нуля; если же этот предел равен нулю, то z называется Б. м. порядка выше k. Изучение порядков различного рода Б. м. — одна из важных задач математического анализа.

Для случая, когда переменная величина есть функция аргумента х, из общего определения предела вытекает такое развёрнутое определение Б. м.: функция f ( x ) , определённая в окрестности точки x 0, называется Б. м. при х, стремящемся к x 0 , если для любого положительного числа e найдётся такое положительное число d, что для всех x ¹ x 0, удовлетворяющих условию |x - x 0| < d, выполняется неравенство |f (x)| < e. Этот факт записывается в виде

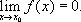
При изучении функции f ( x ) вблизи точки x o за главную Б. м. принимают приращение независимого переменного D х = х - х 0. Формула

D y = f’ ( x 0 ) D x + о (Dх)

выражает, например, что приращение D y дифференцируемой функции с точностью до Б. м. порядка выше первого совпадает с её дифференциалом dy = f ' ( x 0 ) D x.

Метод Б. м., или (что то же) метод пределов, является в настоящее время основным методом обоснования математического анализа, почему его и называют также анализом Б. м. Он заменил исчерпывания метод древних и «неделимых» метод. Метод Б. м. был намечен И. Ньютоном (1666) и получил всеобщее признание после работ О. Коши. При помощи Б. м. даются определения таких основных понятий анализа, как сходящийся ряд, интеграл, производная, дифференциал. Кроме того, метод Б. м. служит одним из основных методов приложения математики к задачам естествознания. Это связано с тем, что большинство закономерностей механики и классической физики выражается в виде формул, связывающих Б. м. приращения изучаемых величин, и обращение к Б. м. является обычным приёмом составления дифференциальных уравнений задачи.

Лит. см. при ст. Анализ математический .

С. Б. Стечкин.

Бесконе'чно удалённые элеме'нтыв математике, элементы (называемые точками, прямыми, плоскостями), которыми пополняется евклидова плоскость или евклидово пространство для интерпретации некоторых разделов математики (проективная геометрия, теория функций комплексного переменного и др.).

Происхождение термина «Б. у. э.» легче всего проследить на следующем примере. Рассмотрим в евклидовой плоскости a ее параллельные прямые а и а' ( рис ., 1) и прямую b , пересекающую их соответственно в точках М и М'. Будем поворачивать прямую b вокруг точки М' в направлении, указанном на рис. стрелкой, до совпадения с прямой а '. Очевидно, по мере приближения прямой b к a' точка М пересечения прямых a и b будет удаляться в бесконечность. Этот процесс достаточно отчетливо поясняет часто употребляемое выражение: «параллельные прямые пересекаются в бесконечно удалённой точке».

Указанные наглядные соображения лежат в основе интерпретации двумерной проективной геометрии на евклидовой плоскости a. Для этой цели плоскость a пополняется бесконечно удалёнными точками и одной бесконечно удалённой прямой следующим образом. Уславливаются рассматривать параллельные прямые как пересекающиеся в бесконечно удалённой точке. Тогда прямая а', параллельная прямой а ( рис ., 2), пересекается с ней в некоторой точке, но только эта точка не является обыкновенной, а представляет собой новый объект — бесконечно удалённую точку прямой а. Уславливаются, что все прямые, параллельные прямой а, имеют одну общую бесконечно удалённую точку А, а бесконечно удалённые точки непараллельных прямых считаются различными. Т. о., евклидова плоскость пополняется бесконечным числом бесконечно удалённых точек. Совокупность всех этих бесконечно удалённых точек плоскости се называют бесконечно удалённой прямой.