БСЭ БСЭ - Большая Советская Энциклопедия (ГА)
- Название:Большая Советская Энциклопедия (ГА)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (ГА) краткое содержание
Большая Советская Энциклопедия (ГА) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Физическая величина, называемая «принуждением», вводится следующим образом. Свободная материальная точка с массой m при действии на неё заданной силы F будет иметь ускорение F/m ; если же на точку наложены связи, то её ускорение при действии той же силы F станет равным какой-то др. величине w . Тогда отклонение точки от свободного движения, вызванное действием связи, будет зависеть от разности этих ускорений, т. e. от F/m—w . Величину Z, пропорциональную квадрату этой разности, и называют «принуждением». Для одной точки
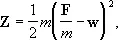
а для механической системы Z равняется сумме таких величин.
Рассмотрим, например, точку, которая начинает двигаться вдоль гладкой наклонной плоскости из положения А без начальной скорости (см. рис. ). Для неё кинематически возможно любое перемещение АВ, AB 1, AB 2 ,... в этой плоскости с какими-то ускорениями w, w 1, w 2 ,..; при свободном же падении точка совершила бы перемещение AC вдоль вертикали с ускорением g . Тогда отклонения точки от свободного движения изобразятся отрезками CB, CB 1, CB 2 ,..., наименьшим из которых будет отрезок CB , перпендикулярный к наклонной плоскости. Следовательно, «принуждение» Z , пропорциональное квадратам CB, CB 1, CB 2 ,..., будет наименьшим при движении вдоль линии наименьшего ската AD . Это и будет истинное движение точки, происходящее с ускорением w = gsina.
Г. п. пользуются для составления уравнений движения механических систем и изучения свойств этих движений.
Лит . см. при ст. Вариационные принципы механики.
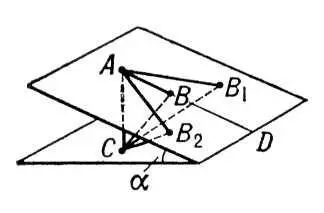
Рис. к ст. Гаусса принцип.
Гаусса распределение
Га'усса распределе'ние, закон распределения вероятностей; то же, что нормальное распределение .
Гаусса система единиц
Га'усса систе'ма едини'ц, система электрических и магнитных величин с основными единицами сантиметр, грамм и секунда, в которой диэлектрическая и магнитная проницаемости являются безразмерными величинами, причём для вакуума они приняты равными единице. Единицы электрических величин в Г. с. е. равны единицам абсолютной электростатической системы СГСЭ, а единицы магнитных величин — единицам абсолютной электромагнитной системы СГСМ, в связи с чем Г. с; е. часто называют симметричной системой СГС (см. СГС система единиц ). Г. с. е. названа в честь К. Гаусса , высказавшего в 1832 идею создания абсолютной системы единиц с основными единицами миллиметр, миллиграмм и секунда и разработавшего эту систему (совместно с В. Вебером ) для измерений магнитных величин.
Лит.: Бурдун Г. Д., Единицы физических величин, 4 изд., M., 1967.
Г. Д. Бурдун.
Гаусса теорема
Га'усса теоре'ма, теорема электростатики , предложенная К. Гауссом и устанавливающая связь потока напряжённости Е электрического поля через замкнутую поверхность с величиной заряда q , находящегося внутри этой поверхности. Потоком вектора Е через элемент поверхности DS i называется произведение величины этого элемента и проекции E ni вектора Е на нормаль к DS i . Поток N через замкнутую поверхность S равен сумме потоков через все элементы поверхности. В абсолютной системе единиц Гаусса (СГС)
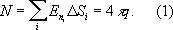
Г. т. вытекает из закона Кулона — закона взаимодействия неподвижных точечных зарядов в вакууме.
В диэлектрике Г. т. справедлива для потока вектора электрической индукции D :
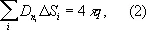
где q — суммарный свободный заряд внутри поверхности S . Формула (2) представляет собой интегральную форму одного из уравнений Максвелла для электромагнитного поля (см. Электродинамика ) и выражает тот факт, что электрические заряды являются источниками электрического поля.
Г. Я. Мякишев.
Гаусса формулы
Га'усса фо'рмулы, формулы, относящиеся к различным разделам математики и носящие имя К. Гаусса.
1) Квадратурные Г. ф. — формулы вида
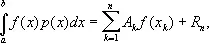
в которых узлы x k и коэффициенты A k не зависят от функции f (x) и выбраны так, что формула точна (т. е. R n = 0) для произвольного многочлена степени 2n - 1 . В отличие от квадратурных формул Ньютона — Котеса, узлы в квадратурных Г. ф., вообще говоря, не являются равноотстоящими. Если р (х) ³ 0 и
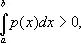
то для любого натурального n имеется единственная квадратурная Г. ф. Эти формулы имеют большое практическое значение, т.к. в ряде случаев они дают значительно большую точность, чем квадратурные формулы с тем же числом равноотстоящих узлов. Сам Гаусс исследовал (1816) случай р (х) º 1 .
2) Г. ф., выражающая полную кривизну К поверхности через коэффициенты её линейного элемента; в координатах, для которых ds 2= l(du 2+ dv 2) , Г. ф. имеет вид
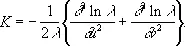
Эта формула была опубликована в 1827 и показывает, что полная кривизна не меняется при изгибании поверхности. Она составляет содержание одного из основных предложений созданной Гауссом внутренней геометрии поверхности.
3) Г. ф. для сумм Гаусса:
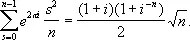
Эта формула была использована Гауссом (1801) в одном из доказательств закона взаимности квадратичных вычетов
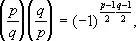
где р и q — нечётные простые числа, а 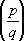 — Лежандра символ . Она явилась первым примером применения метода тригонометрических сумм в теории чисел. Этот метод был развит далее в работах Г. Вейля и особенно И. М. Виноградова и представляет собой один из наиболее мощных методов аналитической теории чисел.
— Лежандра символ . Она явилась первым примером применения метода тригонометрических сумм в теории чисел. Этот метод был развит далее в работах Г. Вейля и особенно И. М. Виноградова и представляет собой один из наиболее мощных методов аналитической теории чисел.
4) Г. ф. для суммы гипергеометрического ряда . Если Re (c - b - a) > 0 , то
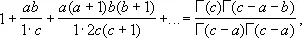
Интервал:
Закладка:
