БСЭ БСЭ - Большая Советская Энциклопедия (ГИ)

Гиперко'мплексные чи'сла, обобщение понятия о числе, более широкое, чем обычные комплексные числа . Смысл обобщения состоит в том, чтобы обычные арифметические действия над такими числами одновременно выражали некоторые геометрические процессы в многомерном пространстве или давали количественное описание каких-либо физических законов. При попытках построить числа, которые играли бы для 3-мерного пространства ту же роль, какую играют комплексные числа для плоскости, выяснилось, что здесь не может быть полной аналогии; это привело к созданию и развитию систем Г. ч.

Г. ч. представляют собой линейные комбинации (с действительными коэффициентами x 1 , x 2 ,. .. ,. x n ) некоторой системы, е 1 , е 2 . .. , e n «базисных единиц»:

x 1e 1 + x 2e 2+ ... + х пе п (*)

подобно тому, как комплексные числа x+iy являются линейными комбинациями двух «базисных единиц»: действительной единицы 1 и мнимой единицы i . Для того чтобы использовать Г. ч., надо в первую очередь установить правила арифметических действий над ними. Сложение и вычитание Г. ч., очевидно, получают однозначное определение, если для новых чисел сохранить обычные правила арифметики; именно, компоненты х 1 , х 2 ,. .. , х п «базисных единиц» должны соответственно складываться или вычитаться. Истинное значение проблемы отчётливо выступает только при установлении правила умножения; для установления почленного перемножения Г. ч. вида (*) приходят к необходимости установить значения n 2 произведений e ie k ( i = 1, 2,..., n ; k = 1, 2,..., n ). Задача состоит в том, чтобы этим произведениям приписать значения вида (*), сохраняющие в силе все обычные правила арифметических операций. Этому требованию удовлетворяет (кроме простейшего случая действительных чисел) единственная система Г. ч. — система комплексных чисел. При установлении же всякой другой системы Г. ч. необходимо отказаться от того или иного правила арифметики; обычно такими правилами, терпящими нарушение, оказываются: однозначность результата деления; переместительность умножения; правило, в силу которого равенство нулю произведения двух чисел влечёт за собой обращение в нуль, по крайней мере, одного из сомножителей, и т.п. Важнейшая система Г. ч. — кватернионы — получается при отказе от коммутативности (переместительности) умножения и сохранения остальных свойств сложения и умножения.

Лит.: Математика, ее содержание, методы и значение, т. 3, М., 1956, гл. 20.

Гиперметаморфо'з(от гипер... и греч. metamorphosis — превращение), сложный способ развития некоторых насекомых (нарывников, веероносцев и некоторых др. жуков, веерокрылых, сетчатокрылых, мух-жужжал и некоторых перепончатокрылых), при котором строение и образ жизни личинок разных возрастов резко различаются. В первом возрасте личинки активно передвигаются, расселяются, но не питаются. Питающиеся личинки старших возрастов обитают в специфической среде (в теле насекомого-хозяина при паразитизме, в запасах пищи пчёл и т.д.). Иногда переход от одной активной формы к следующей требует перестройки, при которой личинка не питается и неподвижна («ложнокуколка», аналогичная куколке ).

М. С. Гиляров.

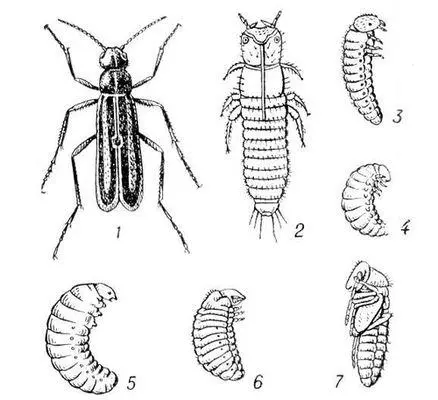
Гиперметаморфоз жука-нарывника Epicanta: 1 — взрослое насекомое; 2 — личинка первого возраста; 3—5 — личинки последующих возрастов; 6 — предкуколка; 7 — куколка.

Гиперметропи'я(от гипер... и греч. metron — мера и ops, родительный падеж opos — глаз), нарушение зрения; то же, что дальнозоркость .

Гиперморфо'з(от гипер... и греч. morphe — вид, форма), гипертелия, сверхспециализация, тип филогенетического развития, ведущий к нарушению отношений организма со средой вследствие гипертрофии отдельных органов (например, клыков у ископаемого саблезубого тигра — махайрода , рогов у гигантского оленя, клыков у современного кабана — бабируссы и т.п.). Частный случай Г. — общее увеличение размеров тела, ведущее к нарушению корреляций отдельных органов. Г. — показатель отставания эволюции организма от изменений условий существования; при значительном проявлении ведёт к вымиранию.

Лит.: Шмальгаузен И. И., Пути и закономерности эволюционного процесса, М. — Л., 1940.

Гипернефро'ма(от гипер... и греч. nephros — почка и -oma — окончание в названиях опухолей), опухоль, развивающаяся из клеток коры надпочечников (истинная Г.) или эпителия почечных канальцев (см. Почки ). Истинная Г. обычно доброкачественная, проявляется извращением вторичных половых признаков ( гирсутизм , вирилизм и др.), гипертонией и повышением температуры тела, у детей — преждевременной половой зрелостью. Лечение хирургическое. Г. почки, опухоль Гравица, почечноклеточный рак — злокачественная опухоль, исходящая из эпителия почки. Впервые описана немецким патологом П. А. Гравицем в 1883. Встречается чаще у мужчин в возрасте 40—60 лет. Лечение хирургическое.

Лит.: Шапиро И. Н., Опухоли почек, лоханок и мочеточников, в кн.: Многотомное руководство по хирургии, отв. ред. Б. В. Петровский, т. 9, М., 1959.

В. М. Вертепова, В. Г. Цомык.

Гиперо'ны(от греч. hypér — сверх, выше), тяжёлые нестабильные элементарные частицы с массой, большей массы нуклона (протона и нейтрона), обладающие барионным зарядом и большим временем жизни по сравнению с «ядерным временем» (~ 10 -23 сек ). Известно несколько типов Г.: лямбда (L 0), сигма (S —, S 0, S +), кси (X —, X 0), омега (W —) [значки —, 0, +справа сверху у символа частиц означают соответственно отрицательно заряженную, нейтральную и положительно заряженную частицы]. Все Г. имеют спин 1/ 2, кроме W —, спин которого, согласно теоретическим представлениям, должен, быть равен 3/ 2(т. е. Г. являются фермионами ). Г. участвуют в сильных взаимодействиях , т. е. принадлежат к классу адронов. Время жизни Г. порядка 10 -10 сек (за исключением S 0, который, по-видимому, имеет время жизни порядка 10 -20 сек ); за это время они распадаются на нуклоны и лёгкие частицы (p-мезоны, электроны, нейтрино).

Г. (L 0) были открыты в космических лучах английскими физиками Рочестером и Батлером в 1947, однако убедительные доказательства существования Г. были получены к 1951. Детальное и систематическое изучение Г. стало возможным после того, как их начали получать на ускорителях заряженных частиц высокой энергии при столкновениях быстрых нуклонов, p-мезонов и К-мезонов с нуклонами атомных ядер.