БСЭ БСЭ - Большая Советская Энциклопедия (ДИ)

Дин Лин(псевдоним; настоящее имя — Цзян Бин-чжи) (р. 1907, провинция Хунань), китайская писательница. Член КПК с 1932. В 1931—32 редактировала журнал Лиги левых писателей Китая «Бэй доу» («Большая Медведица»). Была заместителем председателя СП Китая. В ранних рассказах — «Мын-кэ» (1927), «Дневник Софьи» (1928), «Домик в Цинюньли» (1929), «Шанхай весной 1930 года» и в романе «Вэй Ху» (1930) Д. Л. реалистически показывает положение китайской женщины в условиях феодально-патриархальных традиций и говорит о путях интеллигенции в революцию. Важной вехой в творчестве Д. Л. явилась повесть «Наводнение» (1931), в которой показаны исторические причины трагической судьбы китайского крестьянства. Д. Л. — участница осуществления земельной реформы в 1946—1947, которой посвятила наиболее значительный роман «Солнце над рекой Сангань» (1948; рус. пер., 1949; Государственная премия СССР, 1952). В творческой манере писательницы сочетаются неторопливость изложения, свойственная китайскому народному роману, с идущими от русской и советской прозы многогранностью жизненного охвата, пафосом борьбы.

Обвинённая в 1957 в «правом» буржуазном уклоне, Д. Л. была сослана на «перевоспитание» в глухие районы страны и дальнейшая её судьба неизвестна.

Соч.: Дин Лин сюаньцзи, Пекин, 1951; Дин Лин дуаньпянь сяошо сюаньцзи, Пекин, 1954; в рус. пер. — Избранное, М., 1954.

Лит.: Эйдлин Л. З., О китайской литературе наших дней, М., 1955; Федоренко Н. Т., Китайская литература, М., 1956.

М. Е. Шнейдер.

Ди'на(от греч. dýnamis — сила), единица силы в СГС системе единиц , равная силе, которая массе в 1 г сообщает ускорение 1 см/сек 2 . Русское обозначение — дин , международное — dyn. Соотношение между Д. и ньютоном (единицей силы в Международной системе единиц ): 1 дин = 10 -5 н .

Дина'мик,распространённое краткое название электродинамического громкоговорителя .

Дина'микав музыке, совокупность явлений, связанных с применением различных степеней силы звучания, громкости. Основные градации силы звучания: piano (в нотах сокращённо р) — тихо, слабо и forte (f) — громко, сильно. Производные от piano в сторону ослабления: pianissimo (рр) — очень тихо, piano-pianissimo (ppp) — чрезвычайно тихо и т.д. (до ррррр); от forte в сторону усиления: fortissimo (ff) — очень громко, forte-fortissimo (fff) — чрезвычайно громко и т.д. (до fffff). Применяются также обозначения mezzo piano (mp) — умеренно тихо и mezzo forte (mf) — умеренно громко. Все эти обозначения относятся к более или менее протяжённым музыкальным отрывкам, в которых выдерживается в общем единая и неизменная степень громкости звучания. Внутри таких отрывков нередко выделяются по громкости отдельные звуки, что обозначается терминами forzato, sforzato и др. (см. Акцент ). В музыке широко используется и постепенное усиление или ослабление звучания. Усиление звучания обозначается термином crescendo (cresc, знак ), ослабление — термином decrescendo или diminuendo (decresc. или dim., знак ). Усиление звучания может вести к новой, более высокой степени выдерживаемой некоторое время громкости, может сменяться ослаблением звучания, образуя вместе с ним динамическую «волну». Для уточнения динамических обозначений к ним могут прибавляться слова meno (меньше, менее), quasi (как бы, подобно), molto (очень), росо (несколько), росо а росо (мало-помалу, постепенно) и т.п.

Градации динамики и их обозначения имеют в музыке лишь относительное значение; абсолютная величина громкости зависит от многих факторов, в том числе от типа инструмента, при ансамблевом исполнении — от количества партий и числа исполнителей на каждую партию, а также от акустических свойств помещения. Так, по абсолютному значению piano на трубе гораздо громче, чем forte вокалиста, громкость звучания piano у целого хора значительно выше, чем у отдельного его участника, и т.п. Абсолютные величины громкости измеряются в акустике и выражаются в фонах (см. Громкость звука ).

Дина'мика звёздных систе'м,то же, что звёздная динамика .

Дина'мика маши'н и механи'змов,раздел теории машин и механизмов, в котором изучается движение механизмов и машин с учётом действующих на них сил. Д. м. и м. решает следующие основные задачи: установление законов движения звеньев механизмов, регулирование движения звеньев, нахождение потерь на трение, определение реакций в кинематических парах, уравновешивание машин и механизмов.

Определение законов движения звеньев механизма по заданным характеристикам внешних сил решают с помощью дифференциальных уравнений движения механической системы или машинного агрегата, состоящего обычно из двигателя, передаточного механизма, рабочей машины и иногда управляющего устройства. Число уравнений равняется числу степеней свободы этой механической системы. В плоских механизмах с одной степенью свободы для удобства решения задачи все силы и массы приводят к одному звену или точке механизма, которые называются звеном приведения или точкой приведения. Условный момент, приложенный к звену приведения, называется моментом приведения. Момент приведения равен совокупности всех моментов и сил, приложенных к звеньям механизма. Условный момент инерции звена приведения называется приведённым моментом инерции. Кинетическая энергия звена приведения равна сумме кинетических энергий всех звеньев механизма. Аналогично определяют приведённые силу и массу в точке приведения ( рис. , а):

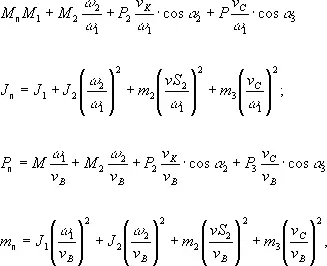
где М п— приведённый момент; J п— приведённый момент инерции; Р п— приведённая сила; m п— приведённая масса; M 1, M 2, P 2, P 3— моменты и силы, приложенные к звеньям механизма; w 1, w 2— угловые скорости звеньев; u B, u C — скорости точек В и С механизма; uS 2— скорость центра тяжести звена 2 ; u K — скорость точки К приложения силы P 2 ; a 2— угол между векторами P 2и u K ; a 3— угол между векторами P 3 и u C . Уравнение движения для данного случая:

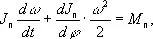
т. е, М пв общем случае зависит от времени, положения, скорости.

Уравнения движения обычно являются нелинейными. Методов точного решения их не существует, поэтому пользуются приближёнными графическими, графо-аналитическими и численными методами интегрирования. Установить закон движения механической системы сложнее, если учитывать трение и зазоры в кинематических парах, упругость и переменность масс звеньев. Иногда, например при изучении быстротекущих процессов в машинах, некоторые внешние силы нельзя считать заданными, т.к. движение механизма может оказать обратное воздействие на характеристику этих сил. Например, в некоторых режимах с большими ускорениями нельзя принимать механическую характеристику электродвигателя как заданную зависимость момента на валу двигателя от угловой скорости, т.к. на этот момент существенное влияние могут оказать электромагнитные процессы в электродвигателе. В этом случае к дифференциальным уравнениям движения механической системы добавляют дифференциальное уравнение электромагнитных процессов в электродвигателе и решают их совместно.