БСЭ БСЭ - Большая Советская Энциклопедия (ИД)

И. называются также идеальными числами. И. — это совокупность чисел, принадлежащих данному числовому кольцу (а в случае произвольного кольца — совокупность его элементов), обладающая следующими свойствами: 1) сумма и разность двух чисел (элементов) совокупности принадлежит этой совокупности; 2) произведение числа (элемента) из этой совокупности на любое другое число (на любой другой элемент) кольца также принадлежит этой совокупности. Затем рассматривают вместо чисел соответствующие им И.; так, например, числу 9 соответствует И. p = (9), состоящий из всех чисел, делящихся на 9.

Числовые понятия, связанные с делимостью чисел, переносятся на И.: один И. делится на другой, если любой элемент первого лежит также и во втором (для чисел это эквивалентно тому, что любое число первого И. делится хотя бы на одно число второго); произведение И. определяется как наименьший И., содержащий всевозможные попарные произведения элементов из обоих идеалов-множителей; наибольший общий делитель двух И. — наименьший И., содержащий элементы как первого, так и второго И., и др. В совокупности целых чисел любой И. состоит из кратных какого-либо фиксированного числа: любой И. является главным. В общем случае, уже для алгебраических иррациональных чисел, не всякий И. является главным. Делимость на главный И. эквивалентна делимости на соответствующее этому И. число. Благодаря наличию не главных И. для целых алгебраических чисел остаётся справедливой теорема о том, что любой И. единственным образом разлагается в произведение неразложимых далее И. Эти неразложимые И., называются также простыми И., выполняют роль простых чисел и характеризуются тем, что обязательно содержат хотя бы один из множителей, если они содержат их произведение. Так, в рассмотренном выше примере

(3) = p 1 p 2,

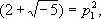
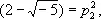
где

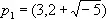
и

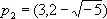
— новые И., например И. p 1, являющийся наибольшим общим делителем И.

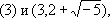
состоит из всех чисел вида

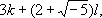
где k и l — любые целые рациональные числа.

Понятие «И.» (или в первоначальной терминологии «идеального числа») было введено в 1847 для одного частного случая числовых полей немецким математиком Э. Куммером. Строгое и полное обоснование теории И. для любых числовых полей дали независимо друг от друга немецкий математик Р. Дедекинд в 1871 и русский математик Е. И. Золотарев в 1877. Новое содержание теория И. получила в середине 20 в. в связи с развитием общей теории колец.

Лит.: Ван-дер-Варден Б. Л., Современная алгебра, пер. с нем., 2 изд., ч. 1—2, М.—Л., 1947.

Идеа'л(франц. idéal, от греч. idéa — идея, первообраз), идеальный образ, определяющий способ мышления и деятельности человека или общественного класса. Формирование природы сообразно И. представляет собой специфически-человеческую форму жизнедеятельности, ибо предполагает специальное создание образа цели деятельности до её фактического осуществления.

Проблема И. была обстоятельно разработана в немецкой классической философии. Наиболее остро она была поставлена И. Кантом в связи с проблемой «внутренней цели». Согласно Канту, явления, не имеющие цели, которая могла бы быть представлена образно, не могут иметь и идеала. Единственным существом, действующим по «внутренней цели», является человек как представитель рода. В животном внутренняя целесообразность осуществляется бессознательно и потому не обретает форму И., особого образа цели. Согласно Канту, И. как воображаемое (достигнутое в воображении) совершенство человеческого рода характеризуется полным и абсолютным преодолением всех противоречий между индивидом и обществом, то есть между индивидами, составляющими «род». Таким образом, осуществление И. совпадало бы с концом истории. В силу этого И., по Канту, принципиально недостижим и представляет собой только «идею» регулятивного порядка. Он указывает скорее направление на цель, чем задаёт образ самой цели, и потому руководит человеком скорее как чувство верного направления, чем как ясный образ результата. Только в искусстве И. может и должен быть представлен в виде образа — в форме прекрасного . И. науки («чистого разума») задаётся в виде принципа «запрета противоречия», моральный И. («практического разума») — в форме категорического императива . Ни там, ни здесь наглядно представить себе состояние, соответствующее И., нельзя, ибо оно неосуществимо в течение сколь угодно длительного, но конечного времени. Поэтому И. и «прекрасное» становятся синонимами, и жизнь И. допускается только в искусстве. Эти идеи Канта получили развитие в соч. Ф. Шиллера , И. Г. Фихте , Ф. В. Шеллинга и немецких романтиков.

Г. Гегель, остро понявший бессилие кантовского представления об И., развенчал его как абстракцию, выражающую на деле один из моментов развивающейся действительности «духа» (то есть истории духовной культуры человечества) и противопоставленную другой такой же абстракции — «эмпирической действительности», якобы принципиально враждебной И. и несовместимой с ним. И. становится у Гегеля моментом действительности, образом человеческого духа, вечно развивающегося через свои имманентные противоречия, преодолевающего свои собственные порождения, свои «отчуждённые» состояния, а не изначально внешнюю и враждебную ему «эмпирическую действительность». И. науки (научного мышления) поэтому может и должен быть задан в виде системы логики, а И. практического разума — в виде образа разумно устроенного государства, а не в виде формальных и принципиально неосуществимых абстрактных императивных требований, обращенных к индивиду. И. как таковой поэтому всегда конкретен, и он постепенно реализуется в истории. Любая достигнутая ступень развития предстаёт с этой точки зрения как частично реализованный И., как фаза подчинения эмпирии власти мышления, силе идеи, творческой мощи понятия, — то есть коллективного разума объединённых вокруг идей людей. В виде И. всегда оформляется образ конкретной цели деятельности «рода», то есть человечества на данной ступени его интеллектуального и нравственного развития. В составе И. действительно представляются разрешенными главные, наиболее острые и окончательно назревшие всеобщие противоречия. «Дух» всегда осуществляет наличные проблемы, а не абстрактно-формальную цель «абсолютного совершенства», представляемого как неподвижное и лишённое жизни (стало быть и противоречий) состояние.