БСЭ БСЭ - Большая Советская Энциклопедия (ИН)

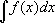
функции f ( x ). Одна из основных теорем интегрального исчисления устанавливает, что каждая непрерывная функция f ( x ) действительного переменного имеет неопределённый И.

Определённый интеграл. Определённый И. функции f ( x ) с нижним пределом а и верхним пределом b можно определить как разность

где F ( x ) есть первообразная функции f ( x ); определение не зависит от того, какая из первообразных выбрана для вычисления определённого И. Если функция f ( x ) непрерывна, то приведённое определение в случае a < b равносильно следующему определению, данному О. Коши (1823): рассматривают произвольное разбиение отрезка [ a , b ] точками

в каждом отрезке [x i— 1, x i ] ( i = 1, 2,. .. , n ) берут произвольную точку x i ( x i— 1£ x i £ x i ) и образуют сумму

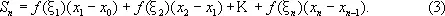
Сумма S n зависит от выбора точек x i и x i . Однако в случае непрерывной функции f ( x ) суммы S n , получающиеся при различном выборе точек x i и x i , стремятся к вполне определённому пределу, если максимальная из разностей x i— x i— 1 стремится к нулю при n ® ¥. Этот предел и является определённым интегралом

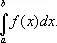
По определению,

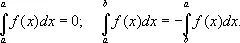
Определённый И., как указано выше, выражается через любую первообразную F ( x ). Обратно, первообразная F ( x ) может быть записана в виде

где а — произвольная постоянная. В соответствии с этим неопределенный И. записывается в виде

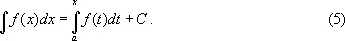
О возникновении понятия И., а также о свойствах неопределенных и определённых И. см. Интегральное исчисление.

Обобщение понятия интеграла

Интеграл Римана. О. Коши применял своё определение И. только к непрерывным функциям. Назвать, по определению, интегралом

предел сумм S n при max ( x i — x i— 1) ® 0 во всех тех случаях, когда этот предел однозначно определён, предложил Б. Риман (1853). Он же исследовал условия применимости такого определения. Более совершенную форму этим условиям придал А. Лебег (1902), пользуясь введённым им понятием меры множества (см. Меры теория ). Для интегрируемости в смысле Римана функции f ( x ) на [ a, b ] является необходимой и достаточной совокупность двух условий: f ( x ) ограничена на [ а, b ], множество помещающихся на [ a , b ] точек разрыва функции f ( x ) имеет меру, равную нулю. Таким образом, непрерывность в каждой точке отрезка [ а , b ] совсем не обязательна для интегрируемости по Риману.

Неопределённый И. и первообразную можно теперь определять формулами (5) и (4). Следует только заметить, что при этом первообразная F ( x ) не обязана иметь подинтегральную функцию f ( x ) своей производной в каждой точке. Но в каждой точке непрерывности f ( x ), т. е., в силу результата Лебега, всюду, кроме, может быть, множества меры, равной нулю, будет

Г. Дарбу (1879) дал определение интеграла Римана, которое делает особенно наглядными условиями существования такого И. Вместо сумм (3) Дарбу вводит суммы (называемые суммами Дарбу)

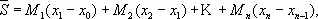
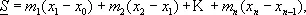
где M k — верхняя грань функции f ( x ) на отрезке [ x k— 1, x k ], а m k— нижняя грань f ( x ) на том же отрезке. Если 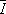нижняя грань сумм 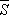, а 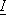— верхняя грань сумм 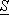, то для существования интеграла Римана необходимо и достаточно условие 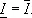Общее значение 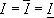величин 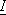и 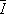и является интегралом Римана (6). Сами величины 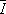и 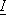называются верхним и, соответственно, нижним интегралами Дарбу.

Интеграл Лебега.Введённое Лебегом понятие меры множества позволило дать значительно более широкое определение И. Чтобы определить И. (6), Лебег делит точками

... < y -2< y -1< y 0< y -1< ... < y i <...

область возможных значений переменного у = f ( x ) и обозначает M i множество тех точек х из отрезка [ a, b ], для которых

y i— 1£ f ( x ) < y i.

Сумма S определяется равенством

S = S ih i m( M i ),

где h i берётся из отрезка y i— 1£ h i < y i , а m( M i ) обозначает меру множества M i. Функция f ( x ) называется интегрируемой в смысле Лебега на отрезке [ a , b ], если ряды, определяющие суммы S , абсолютно сходятся при max( y i— y i— 1) ® 0. Предел этих сумм и называется интегралом Лебега (6). Можно определить первообразную в смысле Лебега как функцию F ( x ), удовлетворяющую равенству (4), где И. в правой части понимается по Лебегу. Как и в случае интеграла Римана, равенство (7) будет при этом выполняться во всех точках, кроме, может быть, множества, имеющего меру, равную нулю.