БСЭ БСЭ - Большая Советская Энциклопедия (ИН)

Для интегрируемости по Лебегу ограниченной функции f ( x ) необходимо и достаточно, чтобы она принадлежала к числу измеримых функций в смысле Лебега. Все функции, встречающиеся в математическом анализе, измеримы в этом смысле. Более того, до настоящего времени (1972) не построено ни одного индивидуального примера неизмеримой функции. Таким образом, для случая ограниченных функций Лебег решил задачу определения интеграла (6) с общностью, исчерпывающей потребности математического анализа. Среди функций, интегрируемых по Лебегу, имеется сколько угодно функций, всюду разрывных и, следовательно, неинтегрируемых по Риману. Наоборот, каждая интегрируемая по Риману функция интегрируема и по Лебегу.

Определение Лебега обобщается на случай интегрирования по полупрямой и по полной прямой, т. е. на случай И. вида

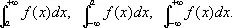
После этого обобщения теория Лебега охватывает все случаи абсолютно сходящихся несобственных интегралов.

Общность, достигнутая в определении Лебега, весьма существенна во многих вопросах математического анализа; например, только с введением интеграла Лебега могла быть установлена теорема Фишера — Риса в теории тригонометрических рядов, в силу которой любой ряд

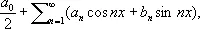
для которого

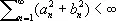
представляет функцию f ( x ), порождающую коэффициенты a n и b n по формулам

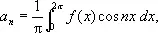
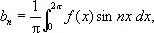
где И. понимаются в смысле Лебега.

Интеграл Стилтьеса.В конце 19 в. определение интеграла Римана подверглось совершенно иному обобщению, чем то, к которому привело введение понятия меры множества. Это обобщение было дано Т. Стилтьесом (1894). Пусть f ( x ) — непрерывная функция действительного переменного х , определённая на отрезке [ a , b ], и U ( x ) — определённая на том же отрезке ограниченная монотонная (неубывающая или невозрастающая) функция. Для определения интеграла Стилтьеса берут произвольное разбиение (2) отрезка [ a , b ] и составляют сумму

f (x 1) [ U ( x 1) — U ( x 0)] + f (x 2) [ U ( x 2) — U ( x 1)] +...+ f (x n ) [ U ( x n ) — U ( x n— 1)], (8)

где x 1, x 2, ..., x n — произвольные точки, выбранные соответственно на отрезках [ x 0, x 1], [ x 1, x 2], ..., [ x n —1, x n ]. Пусть d — наибольшее расстояние между двумя последовательными точками деления в разбиении (2). Если взять любую последовательность разбиений, для которой d стремится к нулю, то сумма (8) будет иметь определённый, всегда один и тот же предел, как бы ни выбирались точки x 1, x 2, ..., x n на соответствующих отрезках. Этот предел называют, следуя Стилтьесу, интегралом функции f ( x ) относительно функции U ( x ) и обозначают символом

Интеграл (9) (его называют также интегралом Стилтьеса) существует и в том случае, когда ограниченная функция U ( x ), не будучи сама монотонной, может быть представлена в виде суммы или разности двух ограниченных монотонных функций U 1( x ) и U 2( x ):

U ( x ) = U 1( x ) — U 2( x ),

т. е. является функцией с ограниченным изменением (см. Изменение функции ).

Если интегрирующая функция U ( х ) имеет ограниченную и интегрируемую по Риману производную U' ( x ), то интеграл Стилтьеса сводится к интегралу Римана по формуле

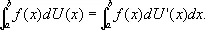
В частности, когда U ( x ) = х + С , интеграл Стилтьеса (9) превращается в обыкновенный интеграл Римана (6).

Дальнейшие обобщения.Концепции И., созданные Стилтьесом и Лебегом, удалось впоследствии объединить и обобщить на интегрирование по любому (измеримому) множеству в пространстве любого числа измерений. Классические кратные интегралы вполне охватываются этим подходом. Потребности таких дисциплин, как теория вероятностей и общая теория динамическим систем, привели к ещё более широкому понятию абстрактного интеграла Лебега, основанному на общих понятиях меры множества и измеримости функций. Пусть Х — пространство, в котором выделена определённая система В его подмножеств, называемых «измеримыми», причём эта система обладает свойствами замкнутости по отношению к обычным теоретико-множественным операциям, выполняемым в конечном или счётном числе. Пусть m — конечная мера, заданная на В. Для В -измеримой функции у = f ( x ), х Î Х , принимающей конечное или счётное число значений y 1, y 2, ..., y n , ..., соответственно на попарно непересекающихся множествах A 1, ..., А n , ..., сумма которых есть X , интеграл функции f ( x ) по мере m, обозначаемый

,

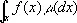определяется как сумма ряда

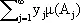
в предположении, что этот ряд абсолютно сходится. Для других f интегрируемость и И. определяются путём некоторого естественного предельного перехода от указанных кусочно постоянных функций.

Пусть А — измеримое множество и j А ( х ) = 1 для х , принадлежащих А , и j А ( х ) = 0 для х, не принадлежащих А . Тогда интеграл от f ( x ) по множеству А определяют, полагая

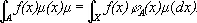
При фиксированных m и А И. в зависимости от f может рассматриваться как линейный функционал ; при фиксированном f И., как функция множества А , есть счётно аддитивная функция.

Следует отметить, что, несмотря на кажущуюся отвлечённость, это общее понятие И. в наибольшей степени подходит для определения такого понятия, как математическое ожидание (в теории вероятностей), и даже для общей формулировки задачи проверки статистических гипотез. И. по отношению к так называемой мере Винера и различным её аналогам используют в статистической физике (здесь в качестве Х фигурирует пространство непрерывных на каком-либо отрезке функций). Упоминавшиеся до сих пор обобщения понятия И. были такими, что f и | f | оказывались интегрируемыми или неинтегрируемыми одновременно.