БСЭ БСЭ - Большая Советская Энциклопедия (ИН)

При этом в работах Ньютона основную роль играло понятие неопределённого интеграла (флюенты, см. Флюксий исчисление ), тогда как Лейбниц исходил из понятия определённого интеграла. Дальнейшее развитие И. и. в 18 в. связано с именами И. Бернулли и особенно Л. Эйлера. В начале 19 в. И. и. вместе с дифференциальным исчислением было перестроено О. Коши на основе теории пределов. В развитии И. и. в 19 в. приняли участие русские математики М. В. Остроградский , В. Я. Буняковский , П. Л. Чебышев . В конце 19 — начале 20 вв. развитие теории множеств и теории функций действительного переменного привело к углублению и обобщению основных понятий И. и. (Б. Риман , А. Лебег и др.).

Лит.: История.Ван дер Варден Б. Л., Пробуждающаяся наука, пер. с голл., М., 1959; Вилейтнер Г., История математики от Декарта до середины 19 столетия, пер. с нем., 2 изд., М., 1966; Строек Д. Я., Краткий очерк истории математики, пер. с нем., 2 изд., М., 1969; Cantor М.. Vorleslingen über Geschichte der Mathematik, 2 Aufl., Bd 3—4, Lpz. — B., 1901—24.

Работы основоположников и классиков И. и.Ньютон И., Математические работы, пер. с латин., М.—Л., 1937; Лейбниц Г., Избранные отрывки из математических сочинений, пер. с. латин., «Успехи математических наук», 1948, т. 3, в. 1; Эйлер Л., Интегральное исчисление, пер. с латин., тт. 1—3, М., 1956—58; Коши О. Л., Краткое изложение уроков о дифференциальном и интегральном исчислении, пер. с франц., СПБ, 1831; его же, Алгебраический анализ, пер. с франц., Лейпциг, 1864.

Учебники и учебные пособия по И. и.Хинчин Д. Я., Краткий курс математического анализа, 3 изд., 1957; Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., т. 2, М., 1969; Ильин В., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; Курант Р., Курс дифференциального и интегрального исчисления, пер. с нем. и англ., 4 изд., т. 1, М., 1967; Двайт Г.-Б., Таблицы интегралов и другие математические формулы, пер. с англ., М., 1964.

Под редакцией академика А. Н. Колмогорова.

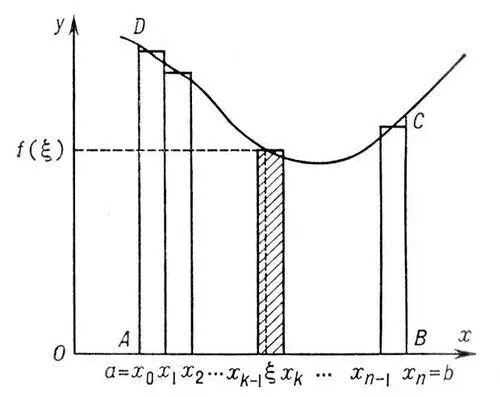
Рис. к ст. Интегральное исчисление.

Интегра'льное стереокино',стереоскопическое кино, в котором объёмно-пространственный образ создаётся в результате одновременной проекции на растровый экран не двух, как в однопарном стереоскопическом кино, а многих плоских взаимосвязанных между собой изображений (кадров), хотя зритель видит из них в каждое мгновение только 2 изображения: одно — левым, а другое — правым глазом. Метод И. с. впервые в мире был предложен в 1962—63 советским изобретателем безочкового стереоскопического кино С. П. Ивановым и совершенствовался им в последующие годы. В 1965 был продемонстрирован экспериментальный кинофильм (режиссер Н. В. Экк), снятый интегральным методом, а в 1972 в Москве (кинотеатр «Октябрь») впервые демонстрировался короткометражный видовой кинофильм «По Южному берегу Крыма», снятый также интегральным методом (режиссёр и оператор Н. И. Большаков).

При наиболее простом способе съёмки И. с. на 8-, 16- или 35- мм киноплёнку применяется обычный (однообъективный) съёмочный аппарат с любыми объективами. В нём изменяется только рамка, ограничивающая поле зрения визира в соответствии с выбранным стереоскопическим экраном. Особенность процесса съёмки заключается в том, что съемочный аппарат устанавливается не обычно, а поворачивается вокруг оптической оси объектива на 90° для обеспечения горизонтального продвижения киноплёнки, необходимого при проекции, и перемещается в горизонтальной плоскости вокруг центрального объекта композиции ( рис. 1 ). Скорость перемещения камеры может быть рассчитана по формуле: v = L × K/ 10×f ' c , где v — скорость движения камеры ( мм/сек ), L — расстояние до центрального объекта композиции ( мм ), К — частота смены кадров ( кадр/сек ), f ' c— сопряжённое фокусное расстояние ( мм ). По этой формуле могут быть составлены таблицы для наиболее характерных или часто встречающихся случаев съёмки. При съёмке допустимы 2—3-кратные отклонения от параметров, указанных в формуле. Простейший контроль правильности такой съёмки заключается в том, что видимые в визире перемещения самых ближних и самых удалённых объектов (относительно неподвижного центрального объекта) от одной границы кадра к другой должны происходить за время не более 10 сек и не менее 2 сек.

При проекции на растровый экран киноплёнка продвигается горизонтально с обычной частотой смены кадров (24 кадр/сек ) мимо нескольких взаимосвязанных объективов. Количество объективов определяется оптическими параметрами растрового экрана. Так, при проекции на растровый экран с перспективным линзовым растром ( рис. 2 ) достаточно от 5 до 10 объективов. В этом случае на любое кресло зрительного зала придется от 5 до 10 элементарных взаимосвязанных фокальных зон, составляющих в целом интегральную зону стереоскопического видения (о фокальных зонах см. в ст. Стереоскопическое кино ). Посредством экрана образуется до 50 интегральных зон или 400—500 элементарных фокальных зон. Такое количество зон обеспечивает нормальные условия просмотра кинофильма зрителем: при отклонении зрителя вправо или влево стереоскопический эффект не пропадает, что неизбежно при однопарной безочковой стереоскопической проекции, а напротив, подчёркивается за счёт естественного перемещения ближних предметов относительно дальних, т. е. в полном соответствии с тем, что наблюдается в жизни.

Однако рассмотренному способу получения И. с. свойствен недостаток: наиболее быстро движущиеся объекты оказываются заснятыми с большим временным параллаксом, проявляющимся при любой проекции в виде дробления изображения движущихся объектов; кроме того, при стереоскопической проекции наблюдается заметная деформация формы объектов и их пространственного положения. Во избежание этого явления предложено 2 более сложных способа получения И. с.: 1) увеличение при съёмке и проецировании частоты смены кадров в 2—4 раза; 2) съёмка и проецирование одновременно серии из 8—9 кадров при прежней частоте смены кадров. Для реализации последнего способа может быть использован киносъёмочный аппарат, в котором применена, например, перфорированная аэрофотоплёнка шириной 190 мм с поперечным (к вертикальному перемещению плёнки) размещением на ней серии из 9 отдельных взаимосвязанных кадров размером 19´19 мм каждый.

Лит.: Иванов Б. Т., Растровая стереоскопия в кино, М., 1945; Валюс Н. А., Растровая оптика, М., 1949; Иванов С.П., Иванов М. С., Быховский В. М. , Интегральная стереодиапроекция на ЭКСПО-70, «Техника кино и телевидения», 1970, № 10, с. 33—38.