БСЭ БСЭ - Большая Советская Энциклопедия (ИН)

Д. А. Васильков.

Интегра'льный логари'фм,специальная функция, определяемая интегралом

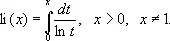
Этот интеграл не выражается в конечной форме через элементарные функции. Если х > 1, то интеграл понимается в смысле главного значения:

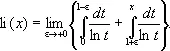
И. л. введён в математический анализ Л. Эйлером в 1768. И. л. li( x ) связан с интегральной показательной функцией Ei( x ) соотношением li( x ) = Ei(ln x ). Для больших положительных х функция li( x ) растет как x / ln x. И. л. играет важную роль в аналитической теории чисел, так как число простых чисел, не превосходящих х, приблизительно равно li( x ).

Лит.: Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968.

Интегра'льный си'нус и интегра'льный ко'синус— специальные функции, определяемые соответственно интегралами

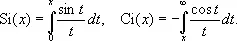
Эти функции введены итальянским математиком Л. Маскерони в 1790. Однако ещё Л. Эйлеру (1781) было известно, что

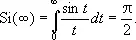
Этот интеграл является простейшим примером сходящегося, но не абсолютно сходящегося несобственного интеграла. Функции Si( x ) и Ci( x ) встречаются в различных вопросах анализа и техники, и для них имеются подробные таблицы.

Лит. см. при ст. Интегральный логарифм .

Интегра'тор,то же, что интегрирующее устройство .

Интегра'ция(биол.), процесс упорядочения, согласования и объединения структур и функций в целостном организме, характерный для живых систем на каждом из уровней их организации. Понятие «И.» ввёл английский учёный Г. Спенсер (1857), связав её с дифференциацией тканей в процессе эволюции и специализацией функций первоначально гомогенной, диффузно реагирующей живой материи. Примеры И. на молекулярном уровне организации: И. аминокислот в сложной молекуле белка, И. нуклеотидов в молекуле нуклеиновой кислоты; на клеточном уровне — оформление клеточного ядра, самовоспроизведение клеток в целом. В многоклеточном организме И. достигает высшего уровня, выражаясь в процессах его онтогенеза; при этом взаимосвязь частей и функций организма возрастает по мере прогрессивной эволюции; система корреляций усложняется, создаются регуляторные механизмы, обеспечивающие устойчивость и целостность развивающегося организма. На уровне сообществ — популяции, видов и биоценозов И. проявляется в сложной и взаимообусловленной эволюции этих биологических систем. Степень И. может служить показателем уровня прогрессивного развития любой живой системы.

В физиологии И. — функциональное объединение частных физиологических механизмов в сложно координированную приспособительную деятельность целостного организма. Элементарная единица И. — функциональная система — динамическое объединение центрально-периферических образований, обеспечивающее саморегуляцию определённой функции. Принципы физиологической И. раскрыл (1906) английский физиолог Ч. Шеррингтон на примере координации рефлекторной деятельности спинного мозга (конвергенция, реципрокность, общий конечный путь и т.д.). Эти принципы действуют на всех уровнях нервной системы, включая кору больших полушарий головного мозга. Высшее проявление физиологической И. — условный рефлекс , в котором психические, соматические и вегетативные компоненты сочетаются в осуществлении целостной приспособительной деятельности организма.

Лит.: Шмальгаузен И. И., Интеграция биологических систем и их саморегуляция, «Бюлл. Московского общества испытателей природы. Отдел биологический», 1961, т. 66, в. 2, с. 104—34; Анохин П. К., Биология и нейрофизиология условного рефлекса, М., 1968.

И. В. Орлов, А. В. Яблоков.

Интегра'ция(лат. integratio — восстановление, восполнение, от integer — целый), понятие теории систем, означающее состояние связанности отдельных дифференцированных частей в целое, а также процесс, ведущий к такому состоянию.

Социальная И. означает наличие упорядоченных отношений между индивидами, группами, организациями, государствами и т. д. При анализе И. различают уровень рассматриваемых систем И. (И. личности, группы, общества и т. д.). При этом термин «интегрированный» имеет различный смысл. Если анализ ведётся на уровне личности (в психологии), под выражением «интегрированная личность» понимается целостный, лишённый внутренних противоречий индивид. То же выражение при анализе на уровне социальной системы относится к личности, интегрированной (включённой) в социальную систему, т. е. к конформной личности. В политической и экономической науках понятие И. может характеризовать внутреннее состояние общества, государства или относиться к государству, интегрированному в более широкую межнациональную общность. И. общества или отдельных государств может осуществляться на основе принуждения, взаимной выгоды или сходства социально-экономического строя, интересов, целей и ценностей различных индивидов, социальных групп, классов, государств. В современных условиях развивается тенденция к межгосударственной И. в экономической и политической областях как в условиях социализма, так и в условиях капитализма. Однако общие объективные предпосылки (научно-техническая революция, тенденция к интернационализации) социалистической и капиталистической И. не означают, что процесс этот в обоих случаях одинаков. Он глубоко различен по социально-экономическим природе, формам, методам, экономическим и политическим последствиям.

Термин «И.» применяется также для характеристики процесса сближения и связи наук, происходящего наряду с процессом их дифференциации .

Л. Л. Седов.

Интегра'ция социалисти'ческая экономи'ческая,сознательно и планомерно регулируемый коммунистическими и рабочими партиями и правительствами стран — членов Совета экономической взаимопомощи (СЭВ) процесс международного социалистического разделения труда, сближения их экономик и формирования современной высокоэффективной структуры национальных хозяйств, постепенного сближения и выравнивания уровней их экономического развития, формирования глубоких и устойчивых связей в основных отраслях экономики, науки и техники, расширения и укрепления международного рынка этих стран, совершенствования товарно-денежных отношений.