БСЭ БСЭ - Большая Советская Энциклопедия (ИН)

И. с. имеет самое широкое применение для измерения длины волны излучения, исследования тонкой структуры спектральной линии, определения плотности, показателей преломления и дисперсионных свойств веществ, для измерения углов, линейных размеров деталей в длинах световой волны, для контроля качества оптических систем и многого другого. На использовании И. с. основано действие интерферометров и интерференционных спектроскопов; метод голографии также основан на И. с.

Важный случай И. с. — интерференция поляризованных лучей (см. Поляризация света ). В общем случае, когда складываются две различно поляризованные когерентные световые волны, происходит векторное сложение их амплитуд, что приводит к эллиптической поляризации. Это явление наблюдается, например, при прохождении линейно поляризованного света через анизотропные среды. Попадая в такую среду, линейно поляризованный луч разделяется на 2 когерентных, поляризованных во взаимно перпендикулярных плоскостях луча. Вследствие различного состояния поляризации скорость их распространения в этой среде различна и между ними возникает разность фаз D, зависящая от расстояния, пройденного в веществе. Величина D будет определять состояние эллиптической поляризации; в частности, при D, равной целому числу полуволн, поляризация будет линейной.

Интерференцию поляризованных лучей широко используют в кристаллооптике для определения структуры и ориентации осей кристалла, в минералогии для определения минералов и горных пород, для обнаружения и исследования напряжений и деформаций в твёрдых телах, для создания особо узкополосных светофильтров и др.

Лит.: Ландсберг Г. С., Оптика. 4 изд., М., 1957 (Общий курс физики, т. 3); Вавилов С. И., Микроструктура света, ч. 2, М., 1950; Борн М., Вольф Э., Основы оптики, пер. с англ., М., 1970.

М. Д. Галанин.

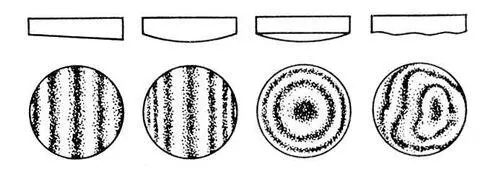
Рис. 4. Типичные случаи полос равной толщины.

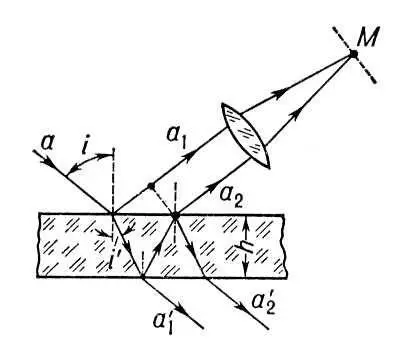
Рис. 3. Интерференция в плоскопараллельной пластинке.

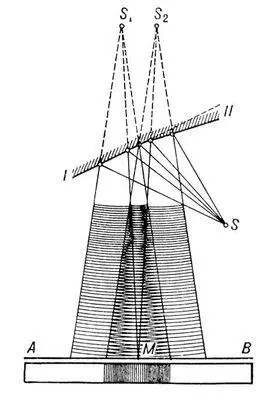
Рис. 1. Схема опыта Френеля.

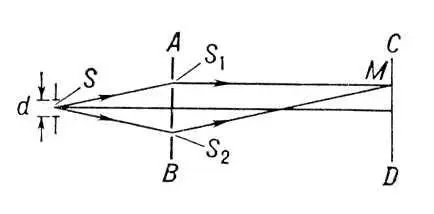
Рис. 2. Схема опыта Юнга.

Интерфере'нция сква'жин,'взаимодействие работающих нефтяных, газовых или водяных скважин, пробурённых с поверхности на один продуктивный пласт или на разные, но гидродинамически связанные друг с другом пласты. И. с. обусловлена тем, что нефть, газ, вода подвижны, а поры продуктивных пластов, в которых они содержатся, связаны в единую систему поровых каналов и трещин. При этом скважины одинакового назначения «мешают» друг другу, перехватывая притекающую к ним жидкость (или газ). В результате дебит каждой из нескольких работающих скважин всегда меньше дебита единичной скважины при прочих равных условиях. Этот факт обусловливает принципиальную особенность разработки месторождений жидких (газообразных) полезных ископаемых: все эксплуатационные нефтяные (газовые или водяные) скважины рассматриваются только в совокупности — в их взаимодействии в общем технологическом процессе разработки. Законы И. с. изучаются специальной наукой о фильтрации — подземной газогидродинамикой.

Интерфере'нцияволн, сложение в пространстве двух (или нескольких) волн, при котором в разных точках получается усиление или ослабление амплитуды результирующей волны. И. характерна для всяких волн независимо от их природы: для волн на поверхности жидкости, упругих (например, звуковых) волн, электромагнитных (например, радиоволн или световых) волн.

Если в пространстве распространяются две волны, то в каждой точке результирующее колебание представляет собой геометрическую сумму колебаний, соответствующих каждой из складывающихся волн. Этот так называемый принцип суперпозиции соблюдается обычно с большой точностью и нарушается только при распространении волн в какой-либо среде, если амплитуда (интенсивность) волн очень велика (см. Нелинейная оптика , Нелинейная акустика ). И. волн возможна, если они когерентны (см. Когерентность ).

Простейший случай И. — сложение двух волн одинаковой частоты при совпадении направления колебаний в складывающихся волнах. В этом случае, если колебания происходят по синусоидальному (гармоническому) закону, амплитуда результирующей волны в какой-либо точке пространства

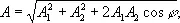
где A 1и A 2— амплитуды складывающихся волн, а j — разность фаз между ними в рассматриваемой точке. Если волны когерентны, то разность фаз j остаётся неизменной в данной точке, но может изменяться от точки к точке и в пространстве получается некоторое распределение амплитуд результирующей волны с чередующимися максимумами и минимумами. Если амплитуды складывающихся волн одинаковы: A 1= A 2, то максимальная амплитуда равна удвоенной амплитуде каждой волны, а минимальная — равна нулю. Геометрические места равной разности фаз, в частности соответствующей максимумам или минимумам, представляют собой поверхности, зависящие от свойств и расположения источников, излучающих складывающиеся волны. В случае двух точечных источников, излучающих сферические волны, эти поверхности — гиперболоиды вращения.

Другой важный случай И. — сложение двух плоских волн, распространяющихся в противоположных направлениях (например, прямой и отражённой). В этом случае получаются стоячие волны .

Среднее за период значение потока энергии в волне пропорционально квадрату амплитуды. Поэтому, как следует из выражения для результирующей амплитуды, при И. происходит перераспределение потока энергии волны в пространстве. Характерное для И. распределение амплитуд с чередующимися максимумами и минимумами остаётся неподвижным в пространстве (или перемещается столь медленно, что за время, необходимое для наблюдений, максимумы и минимумы не успевают сместиться на величину, сравнимую с расстоянием между ними) и его можно наблюдать только в случае, если волны когерентны. Если волны не когерентны, то разность фаз j быстро и беспорядочно изменяется, принимая все возможные значения, так что среднее значение cos j = 0. В этом случае среднее значение амплитуды результирующей волны оказывается одинаковым в различных точках, максимумы и минимумы размываются и интерференционная картина исчезает. Средний квадрат результирующей амплитуды при этом равен сумме средних квадратов амплитуд складывающихся волн, т. е. при сложении волн происходит сложение потоков энергии или интенсивностей.