БСЭ БСЭ - Большая Советская Энциклопедия (ИН)

Нет никакой простой формулы, выражающей точный минимум H’ среднего числа двоичных знаков, необходимого для кодирования сообщении x 1, x 2,..., x n через вероятности p 1, p 2,..., p n этих сообщений. Однако указанный минимум не меньше величины

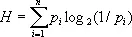
(где log 2 a обозначает логарифм числа a при основании 2) и может превосходить её не более чем на единицу. Величина Н (энтропия множества сообщений) обладает простыми формальными свойствами, а для всех выходов И. т., которые носят асимптотический характер, соответствуя случаю H’ ® ¥, разница между H и H’ абсолютно несущественна. Поэтому именно энтропия принимается в качестве меры неопределённости сообщений данного источника. В приведённом выше примере энтропия равна

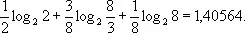
С изложенной точки зрения, энтропия бесконечной совокупности оказывается, как правило, бесконечной. Поэтому в применении к бесконечным совокупностям поступают иначе. Именно, задаются определённым уровнем точности и вводят понятие e — энтропии, как энтропии сообщения, записываемого с точностью до e, если сообщение представляет собой непрерывную величину или функцию (например, времени); подробнее см. в ст. Энтропия .

Так же как и понятие энтропии, понятие количества информации, содержащейся в одном случайном объекте (случайной величине, случайном векторе, случайной функции и т. д.) относительно другого, вводится сначала для объектов с конечным числом возможных значений. Затем общий случай изучается при помощи предельного перехода. В отличие от энтропии, количество информации, например, в одной непрерывно распределённой случайной величине относительно другой непрерывно распределённой величины очень часто оказывается конечным.

Понятие канала связи (см. Канал ) в И. т. носит весьма общий характер. По сути дела, канал связи задаётся указанием множества «допустимых сообщений» на «входе канала», множеством «сообщений на выходе» и набором условных вероятностей получения того или иного сообщения на выходе при данном входном сообщении. Эти условные вероятности описывают влияние «помех», искажающих передаваемые сообщения, «Присоединяя» к каналу какой-либо источник сообщений, можно рассчитать количество информации относительно сообщения на входе, содержащееся в сообщении на выходе. Верхняя грань таких количеств информации, взятая по всем допустимым источникам, называется пропускной способностью (ёмкостью) канала. Ёмкость канала — его основная информационная характеристика несмотря на влияние (возможно сильное) помех в канале, при определённом соотношении между энтропией поступающих сообщений и пропускной способностью канала возможна почти безошибочная передача (при надлежащем кодировании, см. Шеннона теорема ).

И. т. отыскивает оптимальные, в смысле скорости и надежности, способы передачи информации, устанавливая теоретические пределы достижимого качества. Как видно из предыдущего, И. т. носит существенно статистический характер, и поэтому значительная часть ее математических методов заимствуется из теории вероятностей.

Основы И. т. были заложены в 1948—49 американским ученым К. Шенноном. В ее теоретические разделы внесен вклад советским учеными А. Н. Колмогоровым и А. Я. Хинчиным, а в разделы, соприкасающиеся с применениями, — В. А. Котельниковым, А. А. Харкевичем и др.

Лит.: Яглом А. М., Яглом И. М., Вероятность и информация, 2 изд., М., 1960; Шэннон К., Статистическая теория передачи электрических сигналов, в кн.: Теория передачи электрических сигналов при наличии помех. Сб. переводов, М., 1953; Голдман С., Теория информации, пер. с англ., М., 1957; Теория информации и её приложения. Сб. переводов, М., 1959; Хинчин А. Я., Понятие энтропии в теории вероятностей, «Успехи математических наук», 1953, т. 8, в. 3; Колмогоров А. Н., Теория передачи информации, М., 1956, (АН СССР. Сессия по научным проблемам автоматизации производства. Пленарное заседание); Питерсон У. У., Коды, исправляющие ошибки, пер. с англ., М., 1964.

Ю. В. Прохоров.

Информа'ции хране'ние,процесс передачи информации во времени, связанный с обеспечением неизменности состояний материального носителя информации (бумаги, фотоплёнки, магнитной ленты, перфокарты и т. п.). В общем случае И. х. основывается на свойстве запоминающего устройства обладать определённой памятью. В частном случае И. х. представляется как хранение документов. И. х. тесно связано с информационным поиском и поэтому должно осуществляться с обязательным соблюдением принципа адресности и предусматривать возможность вывода информации из запоминающего устройства и её воспроизведения в той или иной форме.

Информа'ции систематиза'ция, классификация документальной информации, один из важнейших видов преобразования документальной информации (в частности, индексирования ), заключающийся в группировке научных документов по отраслям знаний (иерархическая классификация), отдельным проблемам, предметам или по каким-либо формальным признакам. См. Классификации библиотечно-библиографические , Предметизация .

Информацио'нная маши'на,цифровая вычислительная машина, предназначенная для механизации и автоматизации процессов хранения, обработки, поиска данных в больших объёмах информации. И. м. автоматически классифицирует информацию и размещает её в определенных местах памяти или снабжает признаками для ускорения процесса её поиска. Отличительные признаки И. м.: наличие разнотипных запоминающих устройств большой ёмкости (до 10 9букв или цифр) с развитой системой обмена данными между отдельными накопителями; обширный набор устройств для ввода и вывода данных, включая текстовые, визуальные и речевые; наличие дистанционной автоматической связи с источниками и потребителями информации; расширенный состав логических операций для поиска; сортировки и обработки информации; возможность многопрограммной работы, наличие математического обеспечения, содержащего информационно-поисковые языки, словари дескрипторов, классификаторы и программы поиска и переработки информации.

Лит.: Батраков В. А., Богатырев В. И., Электронные цифровые машины для решения информационно-логических задач, М.—Л., 1961; Белоногов Г. Г., Котов Р. Г., Автоматизированные информационно-поисковые системы, М., 1968.