БСЭ БСЭ - Большая Советская Энциклопедия (ИН)

Пример 3 а. Среднее арифметическое результатов наблюдений также содержит некоторую И. относительно рассматриваемой величины. Как показывает математическая статистика, в случае нормального распределения вероятностей ошибок с известной дисперсией среднее арифметическое содержит всю И.

Пример 4. Пусть результатом некоторого измерения является случайная величина X . При передаче по некоторому каналу связи X искажается, в результате чего на приёмном конце получают величину Y = X + q, где q не зависит от X (в смысле теории вероятностей). «Выход» Y даёт И. о «входе» X ; причём естественно ожидать, что эта И. тем меньше, чем больше дисперсия случайной ошибки q.

В каждом из приведённых примеров данные сравнивались по большей или меньшей полноте содержащейся в них И. В примерах 1—3 смысл такого сравнения ясен и сводится к анализу равносильности или неравносильности некоторых соотношений. В примерах 3 а и 4 этот смысл требует уточнения. Это уточнение даётся, соответственно, математической статистикой и теорией И. (для которых эти примеры являются типичными).

В основе теории информации лежит предложенный в 1948 американским учёным К. Шенноном способ измерения количества И., содержащейся в одном случайном объекте (событии, величине, функции и т. п.) относительно другого случайного объекта. Этот способ приводит к выражению количества И. числом. Положение можно лучше объяснить в простейшей обстановке, когда рассматриваемые случайные объекты являются случайными величинами, принимающими лишь конечное число значений. Пусть X — случайная величина, принимающая значения x 1, x 2,..., x n с вероятностями p 1, p 2,..., p n, а Y — случайная величина, принимающая значения y 1, y 2,..., y m с вероятностями q 1, q 2,..., q m . Тогда И. I ( X , Y ) относительно Y , содержащаяся в X , определяется формулой

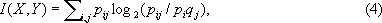
где p ij — вероятность совмещения событий X = x i и Y = y j и логарифмы берутся по основанию 2. И. I ( X , Y ) обладает рядом свойств, которые естественно требовать от меры количества И. Так, всегда I ( X , Y ) ³ 0 и равенство I ( X , Y ) = 0 возможно тогда и только тогда, когда p ij = p iq j при всех i и j, т. е. когда случайные величины X и Y независимы. Далее, всегда I ( X , Y ) £ I ( Y , Y ) и равенство возможно только в случае, когда Y есть функция от X (например, Y = X 2и т. д.). Кроме того, имеет место равенство I ( X , Y ) = I ( Y , X ).

Величина

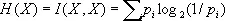
носит название энтропии случайной величины X . Понятие энтропии относится к числу основных понятий теории И. Количество И. и энтропия связаны соотношением

I ( X , Y ) = H ( X ) + H ( Y ) — H ( X , Y ), (5)

где H ( X , Y ) — энтропия пары ( X , Y ), т. е.

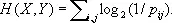
Величина энтропии указывает среднее число двоичных знаков (см. Двоичные единицы ), необходимое для различения (или записи) возможных значений случайной величины (подробнее см. Кодирование , Энтропия ). Это обстоятельство позволяет понять роль количества И. (4) при «хранении» И. в запоминающих устройствах. Если случайные величины X и Y независимы, то для записи значения X требуется в среднем H ( X ) двоичных знаков, для значения Y требуется H ( Y ) двоичных знаков, а для пары ( X , Y ) требуется Н ( Х ) + H ( Y ) двоичных знаков. Если же случайные величины X и Y зависимы, то среднее число двоичных знаков, необходимое для записи пары ( X , Y ), оказывается меньшим суммы Н ( Х ) + H ( Y ), так как

H ( X , Y ) = H ( X ) + H ( Y ) — I ( X , Y ).

С помощью значительно более глубоких теорем выясняется роль количества И. (4) в вопросах передачи И. по каналам связи. Основная информационная характеристика каналов, так называемая пропускная способность (или ёмкость), определяется через понятие «И.» (подробнее см. Канал ).

Если X и Y имеют совместную плотность p ( x , y ), то

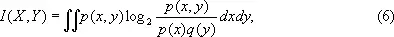
где буквами р и q обозначены плотности вероятности Х и Y соответственно. При этом энтропии Н ( X ) и Н ( Y ) не существуют, но имеет место формула, аналогичная (5),

I ( X , Y ) = h ( X ) + h ( Y ) — h ( X , Y ), (7)

где

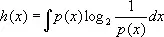
дифференциальная энтропия X [ h ( Y ) и h ( X , Y ) определяется подобным же образом].

Пример 5. Пусть в условиях примера 4 случайные величины X и q имеют нормальное распределение вероятностей с нулевыми средними значениями и дисперсиями, равными соответственно s 2 х и s 2 q . Тогда, как можно подсчитать по формулам (6) или (7):

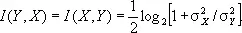
Таким образом, количество И. в «принятом сигнале» Y относительно «переданного сигнала» X стремится к нулю при возрастании уровня «помех» q (т. е. при s 2 q ® ¥) и неограниченно возрастает при исчезающе малом влиянии «помех» (т. е. при s 2 q ® 0).

Особенный интерес для теории связи представляет случай, когда в обстановке примеров 4 и 5 случайные величины X и Y заменяются случайными функциями (или, как говорят, случайными процессами) X ( t ) и Y ( t ), которые описывают изменение некоторой величины на входе и на выходе передающего устройства. Количество И. в Y ( t ) относительно X ( t ) при заданном уровне помех («шумов», по акустической терминологии) q( t ) может служить критерием качества самого этого устройства (см. Сигнал , Шеннона теорема ).

В задачах математической статистики также пользуются понятием И. (сравни примеры 3 и 3а). Однако как по своему формальному определению, так и по своему назначению оно отличается от вышеприведённого (из теории И.). Статистика имеет дело с большим числом результатов наблюдений и заменяет обычно их полное перечисление указанием некоторых сводных характеристик. Иногда при такой замене происходит потеря И., но при некоторых условиях сводные характеристики содержат всю И., содержащуюся в полных данных (разъяснение смысла этого высказывания даётся в конце примера 6). Понятие И. в статистике было введено английским статистиком Р. Фишером в 1921.