БСЭ БСЭ - Большая Советская Энциклопедия (ИЗ)

Соч.: Моя жизнь. Моя работа, Хар., 1934.

Лит.: Сенин Г., Никита Изотов, М. — Хар., 1951.

Н. А. Изотов.

Изотони'ческие раство'ры(от изо... и греч. tónos — напряжение), растворы с одинаковым осмотическим давлением ; в биологии и медицине — природные или искусственно приготовленные растворы с таким же осмотическим давлением, как и в содержимом животных и растительных клеток, в крови и тканевых жидкостях. В нормально функционирующих животных клетках внутриклеточное содержимое обычно изотонично внеклеточной жидкости. При сильном нарушении изотоничности растворов в растительной клетке и окружающей среде вода и растворимые вещества свободно перемещаются в клетку или обратно, что может привести к расстройству нормальных функций клетки (см. Плазмолиз , Тургор ) . Как правило, по своему составу и концентрации И. р. близки к морской воде. Для теплокровных животных изотоничны 0,9%-ный раствор NaCl и 4,5%-ный раствор глюкозы. И. р., близкие по составу, pH, буферности и другим свойствам к сыворотке крови, называются физиологическими растворами (раствор Рингера для холоднокровных животных и растворы Рингера — Локка и Рингера — Тироде для теплокровных животных). В кровезамещающие И. р. для создания коллоидно-осмотического давления вводят высокомолекулярные соединения (декстран, поливинол и др.). Ср. Гипертонические растворы. Гипотонические растворы .

А. А. Булычев, В. А. Соловьев.

Изотони'ческое мы'шечное сокраще'ние,сокращение мышцы при неизменном напряжении, выражающееся в уменьшении её длины и увеличении поперечного сечения. В организме И. м. с. в чистом виде не наблюдается. К чисто И. м. с. приближается движение ненагруженной конечности; при постепенном увеличении груза до тех пор, когда он уже не может быть поднят, удаётся наблюдать все переходы от И. м. с. к изометрическому мышечному сокращению .

Изотони'я,относительное постоянство осмотического давления в жидких средах и тканях организма; то же, что изоосмия .

Изото'ны,атомы различных химических элементов с одинаковым числом нейтронов в ядрах. Пример И. — атомы 5 2Не, 6 3Li, 7 4Be, 8 5В, ядра которых содержат 3 нейтрона. Из этих И. 5He распадается практически мгновенно, 6Li — стабилен, 7Be и 8B — радиоактивны с периодом полураспада соответственно 43 дня и 0,8 сек. См. Изотопы , Ядро атомное .

Изотопи'ческая инвариа'нтность,свойство сильных взаuмoдействий элементарных частиц. Существующие в природе частицы, обладающие сильными взаимодействиями (адроны), можно разбить на группы «похожих» частиц, в каждую из которых входят частицы с примерно равными массами и одинаковыми внутренними характеристиками ( спином , барионным зарядом , странностью ), за исключением электрического заряда. Такие группы называются изотопическими мультиплетами. Оказывается, что сильное взаимодействие для всех частиц, входящих в один и тот же изотопический мультиплет, одинаково, т. е. не зависит от электрического заряда, — в этом и состоит симметрия сильных взаимодействий, называемая И. и.

Простейший пример частиц, которые могут быть объединены в один изотопический мультиплет, — протон (р) и нейтрон (n). Опыт показывает, что сильное взаимодействие протона с протоном, нейтрона с нейтроном и протона с нейтроном одинаково (если они находятся соответственно в одинаковых состояниях); это послужило исходным пунктом для установления И. и. Протон и нейтрон рассматриваются как два разных зарядовых состояния одной частицы — нуклона; они образуют изотопический дублет. Другие примеры изотопических мультиплетов: пи-мезоны (p +, p 0, p -) и S -гипероны (S +, S°, S -), образующие изотопические триплеты.

Электрический заряд Q частицы, входящей в изотопический мультиплет, выражается формулой Гелл-Мана — Нишиджимы:

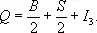
Здесь В — барионный заряд, S — странность (одинаковые для всех частиц в данном изотопическом мультиплете), а величина I 3пробегает с интервалом в единицу все значения от некоторого максимального значения I (целого или полуцелого) до минимального, равного — I : I 3= I , I — 1, ..., — I . Общее число значений, которые может принимать величина I 3(и Q ) для данного изотопического мультиплета, а следовательно, и число частиц в изотопическом мультиплете, равно 2 I + 1. Величина I , определяющая число частиц в изотопическом мультиплете, называется изотопическим спином, а величина I 3— «проекцией» изотопического спина. Эти названия основаны на формальной математической аналогии с обычным спином частиц, поскольку, согласно квантовой механике, для частиц со спином J проекция спина на произвольное направление в пространстве может принимать через единицу значения от + J до — J , т. е. иметь 2 J + 1 значений.

Так как нуклоны существуют в двух зарядовых состояниях, то для них (как и для всех других частиц, входящих в изотопические дублеты) 2 I + 1 = 2, т. е. I = 1/ 2а I 3может принимать два значения: + 1/ 2для протона (что соответствует Q = + 1 , так как у нуклонов барионный заряд B = 1 , а странность S = 0) и — 1/ 2 для нейтрона ( Q = 0). Изотопическому триплету пионов соответствует I = 1, а I 3равно + 1 для p +, 0 для p° и — 1 для p —.Частицы с I = 0 не имеют изотопических «партнёров» и являются изотопическими синглетами; к таким частицам относятся, например, гипероны L 0и W - .

Изотопический спин является, таким образом, важной характеристикой адрона — квантовым числом, показывающим, какое количество изотопических «партнёров» имеет данная частица (или в каком числе зарядовых состояний она может находиться).

На основе И. и. удаётся предсказать существование, массу и заряды новых частиц, если известны их изотопические «партнёры». Так было предсказано существование p°, S°, X° по известным p +, p —; S +, S —и X —.

И. и. имеет место и для составных систем из адронов, в частности для атомных ядер. Изотопический спин сложной системы складывается из изотопических спинов входящих в систему частиц, при этом сложение производится по тем же правилам, что и для обычного спина. Так, система из двух частиц с изотопическими спинами 1/ 2(например, нуклон) и 1 (например, p-мезон) может иметь изотопический спин I = 1 + 1/ 2= 3/ 2или I = 1 — 1/ 2= 1/ 2.