БСЭ БСЭ - Большая Советская Энциклопедия (КА)

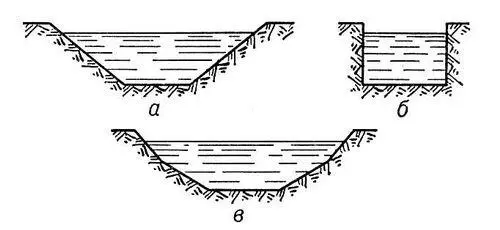
Рис. 3. Формы поперечного сечения каналов: а — трапецеидальная; б — прямоугольная; в — полигональная.

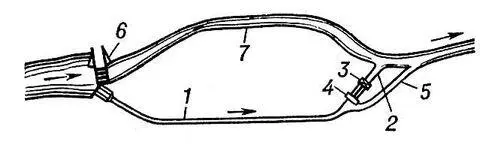
Рис. 2. Схема ГЭС деривационного типа: 1 — деривационный подводящий канал; 2 — деривационный отводящий канал; 3 — здание ГЭС; 4 — напорный бассейн; 5 — водосбросный канал; 6 — головной водозаборный узел; 7 — река.

Рис. 5б. Ирригационный канал Сан-Луис (США, Калифорния).

Рис. 5в. Канал им. Москвы (СССР).

Рис. 4. Облицовка ложа канала бетонными плитами.

Рис. 5а. Северо-Крымский магистральный канал (СССР).

Рис. 5д. Сайменский канал (Финляндия).

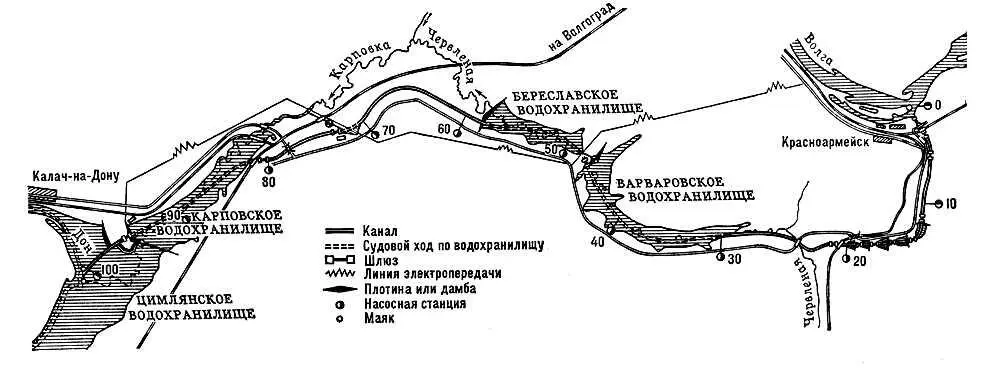
Рис. 1. Волго-Донской судоходный канал имени В. И. Ленина. Общая схема.

Рис. 5г. Северный канал (Франция).

Кана'лв теории информации, всякое устройство, предназначенное для передачи информации. В отличие от техники, информации теория отвлекается от конкретной природы этих устройств, подобно тому как геометрия изучает объёмы тел, отвлекаясь от материала, из которого они изготовлены (ср. Канал информационный). Различные конкретные системы связи рассматриваются в теории информации только с точки зрения количества информации, которое может быть надёжно передано с их помощью. Т. о. приходят к понятию К.: канал задаётся множеством «допустимых» сообщений (или сигналов) x на входе, множеством сообщений (сигналов) у на выходе и набором условных вероятностей р (у|х) получения сигнала у на выходе при входном сигнале х. Условные вероятности р (у|х) описывают статистические свойства «шумов» (помех), искажающих сигналы в процессе передачи. В случае, когда р (у|х) = 1 при у = х и р (y|x) = 0 при у ¹ х, К. называют каналом без «шумов». В соответствии со структурой входных и выходных сигналов выделяют К. дискретные и К. непрерывные. В дискретных К. сигналы на входе и на выходе представляют собой последовательности «букв» из одного и того же или различных «алфавитов» (см. Код ) . В непрерывных К. входной и выходной сигналы суть функции непрерывного параметра t — времени. Возможны также смешанные случаи, но обычно в качестве идеализации предпочитают рассматривать один из указанных двух случаев.

Способность К. передавать информацию характеризуется некоторым числом — пропускной способностью, или ёмкостью, К., которое определяется как максимальное количество информации относительно сигнала на входе, содержащееся в сигнале на выходе (в расчёте на единицу времени).

Точнее: пусть входной сигнал x принимает некоторые значения х с вероятностями р ( х ) . Тогда по формулам теории вероятностей можно рассчитать как вероятности q ( y ) того, что сигнал h на выходе примет значение у:

так и вероятности р (х, y) совмещения событий x = х, h = у:

р (х, у) = р (х) р (у|х).

По этим последним вычисляется количество информации (в двоичных единицах) 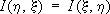и его среднее значение

,

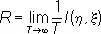где T — длительность x. Верхняя граница С величин R, взятая по всем допустимым сигналам на входе, называют ёмкостью К. Вычисление ёмкости, подобно вычислению энтропии, легче в дискретном случае и значительно сложнее в непрерывном, где оно основывается на теории стационарных случайных процессов.

Проще всего положение в случае дискретного К. без «шумов». В теории информации устанавливается, что в этом случае общее определение ёмкости С равносильно следующему:

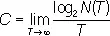
где N ( T ) — число допустимых сигналов длительностью Т.

Пример 1. Пусть «алфавит» К. без «шумов» состоит из двух «букв» — 0 и 1, длительностью t сек каждая. Допустимые сигналы длительностью Т = nt представляются последовательностями символов 0 и 1. Их число N (Т) = 2 n . Соответственно

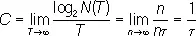— двоичных единиц/ сек .

Пример 2. Пусть символы 0 и 1 имеют длительность t и 2t сек соответственно. Здесь допустимых сигналов длительностью Т = nt будет меньше, чем в примере 1. Так, при n = 3 их будет всего 3 (вместо 8). Можно подсчитать теперь

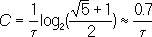двоичных единиц/ сек .

При необходимости передачи записанных с помощью некоторого кода сообщений по данному К. приходится преобразовывать эти сообщения в допустимые сигналы К., т. е. производить надлежащее кодирование. После передачи надо произвести операцию декодирования, т. е. операцию обратного преобразования сигнала в сообщение. Естественно, что кодирование целесообразно производить так, чтобы среднее время, затрачиваемое на передачу, было возможно меньше. При одинаковой длительности символов на входе К. это означает, что надо выбирать наиболее экономный код с «алфавитом», совпадающим с входным «алфавитом» К.

При описанной процедуре «согласования» источника с К. возникает специфическое явление задержки (запаздывания), которое может пояснить следующий пример.

Пример 3. Пусть источник сообщений посылает через промежутки времени длиной 1/u (т. е. со скоростью u) независимые символы, принимающие значения x 1, x 2, x 3, x 4 с вероятностями, равными соответственно 1/ 2, 1/ 4, 1/ 8, 1/ 8. Пусть К. без «шумов» такой же, как в примере 1, и кодирование осуществляется мгновенно. Полученный сигнал или передаётся по К., если последний свободен, или ожидает (помещается в «память») до тех пор, пока К. не освободится. Если теперь выбран, например, код x 1= 00 , x 2 = 01 , x 3 = 10 , x 4 = 11 и u £ 1/ 2t (т. е. 1/u ³ 2t ), то за время между появлением двух последовательных значений х кодовое обозначение успевает передаться и К. освобождается. Т. о., здесь между появлением какой-либо «буквы» сообщения и передачей ее кодового обозначения по К. проходит промежуток времени 2t. Иная картина наблюдается при u > 1/ 2t ; n -я «буква» сообщения появляется в момент (n — 1)/u и её кодовое обозначение будет передано по К. в момент 2nt. Следовательно, промежуток времени между появлением n -й «буквы» сообщения и моментом её получения после декодирования переданного сигнала будет больше, чем n (2t — 1/u) , что стремится к бесконечности при n ® ¥. Таким образом, в этом случае передача будет вестись с неограниченным запаздыванием. Стало быть, для возможности передачи без неограниченного запаздывания при данном коде необходимо и достаточно выполнение неравенства u £ 1/ 2t . Выбором более удачного кода можно увеличить скорость передачи, сделав её сколь угодно близкой к ёмкости К., но эту последнюю границу невозможно превзойти (разумеется, сохраняя требование ограниченности запаздывания). Сформулированное утверждение имеет совершенно общий характер и называется основной теоремой о К. без «шумов».