БСЭ БСЭ - Большая Советская Энциклопедия (КО)

К. наземных позвоночных состоят из трёх отделов: плеча (в передних) или бедра (в задних), сочленяющихся с поясом К., предплечья (в передней) или голени (в задней) с двумя костями в каждой (соответственно—локтевая и лучевая, малая и большая берцовые) и кисти (в передних) или стопы (в задних), состоящих из большого числа мелких косточек, группирующихся в передней К. в запястье, пясть и фаланги пальцев, а в задней — в предплюсну, плюсну и также фаланги пальцев. В ходе эволюции парные К. подверглись значительным преобразованиям. Развитие полёта у летающих ящеров, птиц и летучих мышей вызвало превращение передних К. в крылья. К. морских ящеров, китообразных, ластоногих стали ластами, внешне напоминающими плавники рыб. Приспособление к быстрому бегу привело к сокращению числа пальцев (до 1 у лошади) и площади опоры К. путём замены стопохождения пальцехождением, а у копытных — даже копытохождением с опорой только на конечную фалангу. К. наземных позвоночных часто выполняют ряд дополнительных функций, например передние К. кротов превратились в органы рытья, а у древесных форм, например К. обезьян, — хватания. В ряде случаев парные К. с утерей функционального значения исчезают: например брюшные плавники угрей, задние К. китообразных и сирен, обе пары К. у безногих земноводных, некоторых ящериц, всех змей.

2) У человека различают верхние и нижние К., причленяющиеся к телу плечевым и тазовым поясом. В связи с переходом предков человека к прямохождению, т. е. хождению только на задних К., передние К. освободились и под влиянием труда преобразовались в совершенные органы, имеющие универсальное назначение, — руки.

В. Б. Суханов.

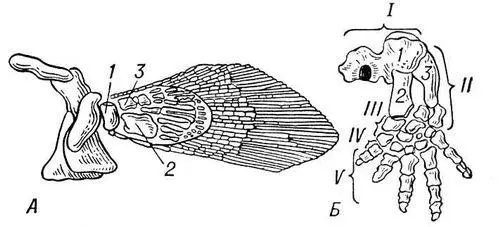
Рис. 2. Преобразование передней конечности при переходе к наземному образу жизни: А — кистепёрая рыба; Б — Древнейшее наземное позвоночное — стегоцефал; 1 — плечевая кость; 2 — лучевая кость; 3 — локтевая кость; I — плечо; II — предплечье; III — запястье; IV — пясть; V — фаланги пальцев.

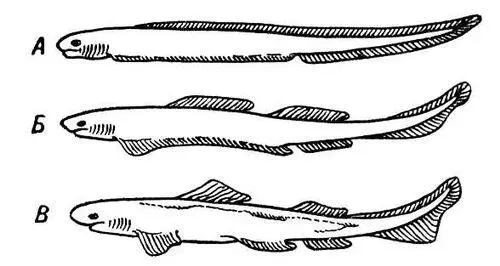
Рис. 1. Три последовательные стадии (А, Б, В) образования непарных и парных плавников (схема).

Коне'чный выключа'тель,концевой, электрический аппарат, обеспечивающий переключения в цепях управления электроприводов машин (механизмов) или их органов в определённых точках движения. К. в. приводится в действие самим перемещающимся механизмом обычно в конце своего движения либо в заданном месте пути следования. Например, в подъёмно-транспортных машинах К. в. отключает электродвигатель и включает тормозное устройство при подходе к конечным точкам пути, что предохраняет механизм от аварии. К. в. бывают контактными и бесконтактными. По конструкции различают нажимные (кнопочные), рычажные, шпиндельные и вращающиеся К. в.

Коне'чных прираще'ний фо'рмула,формула Лагранжа, одна из основных формул дифференциального исчисления, дающая связь между приращением функции f(x) и значениями её производной, эта формула имеет вид:

f(b)-f(a)=(b-a)f’(c), (1)

где с — некоторое число, удовлетворяющее неравенствам a<���с Формула (1) справедлива, если функция f(x) непрерывна на отрезке [ a , b ] и имеет производную в каждой точке интервала (а, b ) . Геометрически формула (1) выражает, что на кривой y = f(x) найдётся точка [ c , f(c) ], касательная в которой параллельна хорде, проходящей через точки [ a, f(a) ] и [ b , f(b) ] . К. п. ф. была открыта Ж. Лагранжем в 1797.

Среди различных обобщений К. п. ф. следует отметить формулу Бонне

,

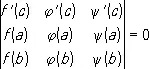её частный случай — формулу Коши

.

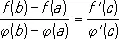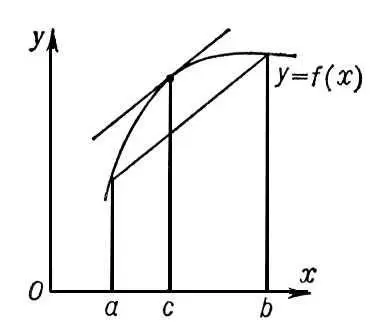
Рис. к ст. Конечных приращений формула.

Коне'чных ра'зностей исчисле'ние,раздел математики, в котором изучаются функции при дискретном (прерывном) изменении аргумента, в отличие от дифференциального исчисления и интегрального исчисления, где аргумент предполагается непрерывно изменяющимся. Конечными разностями «вперёд» для последовательности значений y 1= f (x 1), y 2= f (x 2),..., y k= f (x k),... функции f (x), соответствующих последовательности значений аргумента x 0,..., x k,,... ( x k = х 0 + kh, h — постоянное, k — целое), называют выражения:

D y kº D f (x k) = f (x k+1) - f (x k)

(разности 1-го порядка),

D 2y kº D 2f (x k) = D f (x k+1)- D f (x k) = f (x k+2)-2f (x k+1) + f (x k)

(разности 2-го порядка),

D ny kº D nf (x k) = D n-1f (x k+1) - D n-1f (x k)

(разности n-го порядка).

Соответственно, конечные разности «назад» D n y к определяются равенствами

D ny к= D ny к + n.

При интерполяции часто пользуются т. н. центральными разностями d ny , которые вычисляются при нечётном n в точках х = x i+ 1l 2h, а при чётном n в точках х = x i по формулам

df (x i+ 1/ 2h) º dy i+1/2= f (x i+1) - f (x i),

d 2f (x i) º d 2y i= dy i+1/2,

d 2m-1f (x i+ 1/ 2h) º d 2т— 1yi +1/2= d 2т— 2yi +1-d 2т— 2yi,

d 2mf (x i) º d 2ту i= d 2т— 1yi +1/2- d 2т— 1yi -1/2

Они дополняются средними арифметическими

,

,

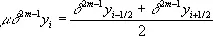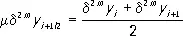где m = 1,2,...; если m = 0, то полагают

.

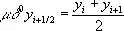Центральные разности d n y связаны с конечными разностями D n y соотношениями

d 2ту i= D 2ту i-m,

d 2т+ 1yi +1/2= D 2m+1y i-m

Если значения аргумента не составляют арифметической прогрессии, т. е. x k+1- x k не есть тождественно постоянная, то вместо конечных разностей пользуются разделёнными разностями, последовательно определяемыми по формулам

…………………………..……………………

.

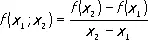
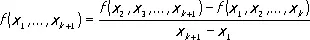Связь между конечными разностями и производными устанавливается формулой D ny k= f (n)( 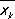), где x k£ 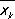£x k+n. Существует полная аналогия между ролью конечных разностей в теории функций дискретного аргумента и ролью производных в теории функций непрерывного аргумента; конечные разности являются удобным аппаратом при построении ряда разделов численного анализа: интерполирование функций, численное дифференцирование и интегрирование, численные методы решения дифференциальных уравнений.