БСЭ БСЭ - Большая Советская Энциклопедия (КО)
- Название:Большая Советская Энциклопедия (КО)
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
БСЭ БСЭ - Большая Советская Энциклопедия (КО) краткое содержание
Большая Советская Энциклопедия (КО) - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Так как в этом случае
Е (Y - y (x)) 2= s 2 Y( 1 - r 2)
и
Е (Y - x (y)) 2= s 2 X( 1 - r 2)
то очевидно, что r (корреляционные отношения совпадают с r 2 полностью определяет степень концентрации распределения вблизи линий регрессии: в предельном случае r = ± 1 прямые регрессии сливаются в одну, что соответствует строгой линейной зависимости между Y и X , при r = 0 величины не коррелированы.
Корреляция между диаметрами и высотами 624 стволов северной сосны
| Диаметр, см | Высота, м | Итого | |||||||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| 14-17 | 2 | 2 | 5 | 1 | 10 | ||||||||||
| 18-21 | 1 | 3 | 3 | 12 | 15 | 9 | 4 | 47 | |||||||
| 22-25 | 1 | 1 | 1 | 3 | 18 | 24 | 29 | 14 | 7 | 98 | |||||
| 26-29 | 7 | 18 | 30 | 43 | 31 | 3 | 2 | 134 | |||||||
| 30-33 | 1 | 5 | 18 | 29 | 35 | 18 | 7 | 1 | 114 | ||||||
| 34-37 | 1 | 3 | 17 | 33 | 26 | 12 | 6 | 98 | |||||||
| 38-41 | 2 | 2 | 10 | 19 | 16 | 4 | 53 | ||||||||
| 42-45 | 4 | 13 | 6 | 8 | 1 | 32 | |||||||||
| 46-49 | 3 | 3 | 7 | 6 | 2 | 1 | 22 | ||||||||
| 50-53 | 1 | 4 | 4 | 2 | 1 | 12 | |||||||||
| 54-57 | 1 | 1 | 1 | 3 | |||||||||||
| 58 и более | 1 | 1 | |||||||||||||
| Итого | 4 | 6 | 9 | 16 | 41 | 57 | 86 | 108 | 124 | 91 | 55 | 24 | 2 | 1 | 624 |
| Средний диаметр | 18,5 | 18,6 | 17,7 | 20,0 | 22,9 | 25,0 | 27,2 | 30,1 | 32,7 | 38,3 | 40,0 | 41,8 | 49,5 | 43,5 | 31,2 |
При изучении связи между несколькими случайными величинами X 1 ,..., X n пользуются множественными и частными корреляционными отношениями и коэффициентами К. (последними по-прежнему в случае линейной связи). Основной характеристикой зависимости являются коэффициенты r ij— простые коэффициенты К. между X i и X j, в совокупности образующие корреляционную матрицу (r ij) (очевидно, r ij= r jiи r kk= 1). Мерой линейной К. между X 1 и совокупностью всех остальных величин X 2,..., X n служит множественный коэффициент К., равный при n = 3
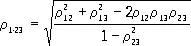 .
.
Если предполагается, что изменение величин X 1 и X 2 определяется в какой-то мере изменением остальных величин X 3, ..., X n, то показателем линейной связи между X 1 и X 2 при исключении влияния X 3,..., X n ; является частный коэффициент К. X 1 и X 2 относительно X 3,..., X n, равный в случае n= 3
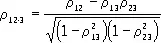
Множественные и частные корреляционные отношения выражаются несколько сложнее.
В математической статистике разработаны методы оценки упомянутых выше коэффициентов и методы проверки гипотез об их значениях, использующие их выборочные аналоги (выборочные коэффициенты К., корреляционные отношения и т. п.). См. Корреляционный анализ.
Лит.: Дунин- Барковский И. В., Смирнов Н. В., Теория вероятностей и математическая статистика в технике (Общая часть), М., 1955; Крамер Г., Математические методы статистики, пер. с англ., М., 1948; Хальд А., Математическая статистика с техническими приложениями, пер. с англ., М., 1956; Ван дер Варден Б. Л., Математическая статистика, пер. с нем., М., 1960; Митропольский А. К., Техника статистических вычислений, 2 изд., М., 1971.
А. В. Прохоров.
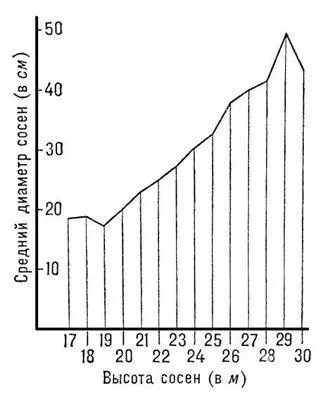
Приближённая линия регрессии для зависимости среднего диаметра северной сосны от высоты.
Корреляция (соотношение)
Корреля'ция(от позднелат. correlatio — соотношение), термин, применяемый в различных областях науки и техники для обозначения взаимозависимости, взаимного соответствия, соотношения понятий, предприятий, предметов, функций. См. также Корреляция в математической статистике, Корреляция в биологии, Корреляция в лингвистике.
Корреляция (стратиграфич.)
Корреля'циястратиграфическая, сопоставление друг с другом одновозрастных слоев осадочных и вулканических горных пород и привязка их к подразделениям единой стратиграфической шкалы; сопоставление может охватывать как отдельные разрезы буровых скважин частных нефтеносных площадей или отдельных месторождений (углей, солей и др.), так и обширные площади и даже нескольких материков (телекорреляция и межконтинентальная К.). При К. используются всевозможные методы сопоставления — прослеживания маркирующих пластов и их пачек, данные каротажа, биостратиграфический метод, изотопные определения возраста горных пород (см. Геохронология ) . В результате К. составляется стратиграфическая схема, в левой части которой наносятся подразделения единой стратиграфической шкалы, а в правой — стратиграфическая схема отложений, встреченных в изучаемом районе.
Корренс Карл Эрих
Ко'рренс(Correns) Карл Эрих (19.9.1864, Мюнхен, — 14.2.1933, Берлин), немецкий ботаник. По окончании Мюнхенского университета получил (1889) степень доктора; с 1897 профессор Тюбингенского, в 1903—07 Лейпцигского, в 1909—14 Мюнстерского университетов. В 1914—33 директор института биологии в Берлине. Основная заслуга К. — вторичное открытие и подтверждение (одновременно с X. Де Фризом и Э . Чермаком) законов наследственности, установленных Г. Менделем. Труды К. посвящены дальнейшему изучению явлении наследственности у растений: ксений, определению пола, пестролистности и плазматической наследственности. К. предвосхитил понимание закономерностей сцепления и обмена наследственных факторов в хромосомах (1902) и менделевского наследования пола у растений.
Соч.: Gesammelte Abhandlungen zur Vererbungswisseiischaft aus periodischen Schriften. 1899—1924, В., 1924; Bestimmung. Vererbung und Verteilung des Geschlechtes bei den höheren Pflanzen, B., 1928; Nicht Mendeinde Vererbung, B., 1937.
Лит.: Roberts Н. F., Plant hybridization before Mendel, Princeton, 1929, p. 335—43; Рижков В., Карл Ерих Корренс, в кн.: Корренс К., Про неменделicтичну спадковicть. К., 1934, с. 5—14; Гайсинович А. Е., Зарождение генетики, М., 1967.
Читать дальшеИнтервал:
Закладка:
