БСЭ БСЭ - Большая Советская Энциклопедия (КО)

Обобщением К. и. являются интегралы типа Коши; они имеют тот же вид, но кривая g не предполагается замкнутой и функция f (t) не предполагается аналитической. Такие интегралы по-прежнему определяют аналитические функции; их значения на g отличаются, вообще говоря, от функции f (t). Систематическое изучение их было начато Ю. В. Сохоцким и впоследствии продолжалось главным образом русскими и советскими математиками (Ю. Г. Колосов, В. В. Голубев, И. И. Привалов, Н. И. Мусхелишвили) как в направлении дальнейших обобщений, так и для приложения к вопросам механики.

Лит.: Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1—2, М., 1967—68; Привалов И. И., Граничные свойства аналитических функций, 2 изд., М.— Л., 1950.

Коши' нера'венство,неравенство для конечных сумм, имеющее вид:

.

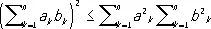Одно из важнейших и наиболее употребительных неравенств. Доказано О. Коши (1821). Интегральный аналог К. н. установлен русским математиком В. Я. Буняковским (см. Буняковского неравенство ) , интересное обобщение К. н. сделано немецким математиком О. Гёльдером (см. Гёльдера неравенство ).

Коши'(Cauchy) Огюстен Луи (21.8.1789, Париж, — 23.5.1857, Со), французский математик, член Парижской АН (1816). Окончил Политехническую школу (1807) и Школу мостов и дорог (1810) в Париже. В 1810—13 работал инженером в г. Шербур. В 1816—30 преподавал в Политехнической школе и Коллеж де Франс. С 1848 в Парижском университете и в Коллеж де Франс. Работы К. относятся к различным областям математики (преимущественно к математическому анализу) и математической физики. Его курсы анализа («Курс анализа», 1821, «Резюме лекций по исчислению бесконечно малых», 1823, «Лекции по приложениям анализа к геометрии», т. 1—2, 1826—28), основанные на систематическом использовании понятия предела, послужили образцом для большинства курсов позднейшего времени. В них он дал определение понятия непрерывности функции, чёткое построение теории сходящихся рядов (см., например Коши — Адамара теорема ), определение интеграла как предела сумм и др. К. систематически развивал основы теории аналитических функций комплексного переменного (см. Коши — Римана уравнения ) , дал выражение аналитической функции в виде интеграла (см. Коши интеграл ) , разложение функции в степенной ряд (см. Коши теорема ) , разработал теорию вычетов. В области теории дифференциальных уравнений К. принадлежат: постановка т. н. Коши задачи, основные теоремы существования решений и метод интегрирования уравнений с частными производными 1-го порядка (метод К. — метод характеристических полос). В работах по теории упругости он рассматривал тело как сплошную среду и оперировал напряжением и деформацией, относимой к каждой точке. В работах по оптике К. дал математическую разработку теории Френеля и теории дисперсии. К. принадлежат также исследования по геометрии (о многогранниках), по теории чисел, алгебре и т. д. По политическим убеждениям К. — ультрароялист, сторонник Бурбонов (после Революции 1830 — в эмиграции до 1838), клерикал.

Соч.: CEuvres complètes, sér . 1, t. 1—12, sér. 2, t. 1—13, P., 1882—1932; в рус. пер. — Алгебраический анализ, Лейпциг, 1864; Краткое изложение уроков о дифференциальном и интегральном исчислении, СПБ, 1831; Исследование о многогранниках, «Успехи математических наук», 1944, в. 10.

Лит.: Бобынин В. В., Огюстен Луи Коши. (Очерк его жизни и деятельности), «Физико-математические науки в их настоящем и прошедшем», 1887, т. 3, № 1—3; Маркушевич А. И., Очерки по истории теории аналитических функций, М.— Л., 1951.

О. Л. Коши.

Коши' распределе'ние,специальный вид распределения вероятностей случайных величин. Введено О. Коши; характеризуется плотностью

p ( x ) = 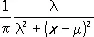, l > 0;

характеристическая функция

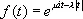
К. р. — унимодально и симметрично относительно точки х = m, являющейся его модой и медианой. Ни один из моментов, К. р. положительного порядка не существует. На рис. дано К. р. при m = 1,5, l = 1.

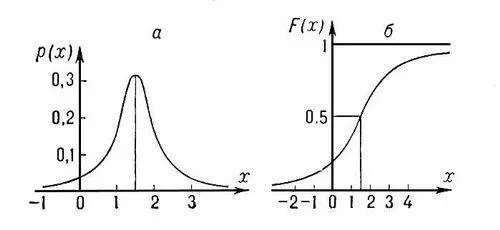
Распределение Коши: а — плотность вероятности; б — функция распределения.

Коши' теоре'мао разложении аналитической функции в степенной ряд. Пусть f (z) — функция, однозначная и аналитическая в области G ; z 0— произвольная (конечная) точка области G и r — расстояние от z 0 до границы этой области. Тогда существует степенной ряд, расположенный по степеням z — z 0, сходящийся в круге | z—z 0 | < r и представляющий в этом круге функцию f (z):

.

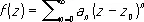Граница области G может сводиться к бесконечно удалённой точке; в этом случае r следует считать равным бесконечности. Эта теорема была установлена О. Коши (1831), исходившим из представления аналитической функции в виде Коши интеграла.

Ко'шице(Košice), город в Чехословакии, в Словацкой Социалистической Республике, административный центр Восточно-Словацкой области. Расположен в долине р. Горнад у подножия Словацкого Рудогорья. 152 тыс. жителей (1971), второй по численности населения город в Словакии. Транспортный узел. Центр чёрной металлургии (см. Восточнословацкий металлургический комбинат ) . Тяжёлое машиностроение, магнезитовая, пищевая, швейная, деревообрабатывающая промышленность. университет. В К. — выдающийся памятник готической архитектуры Словакии — собор святой Елизаветы (1382—1499) с богатой каменной резьбой, готическая капелла святого Михаила (2-я половина 14 в.), доминиканские церковь и монастырь (14—18 вв.), барочная ратуша (1756), дворцы и общественные здания в стиле классицизма. С конца 1940-х гг. ведётся широкое жилищное строительство. Музей Восточной Словакии.

Ко'шицкая програ'мма,программа первого правительства Национального фронта чехов и словаков, разработанная компартией Чехословакии. Провозглашена 5 апреля 1945 в г. Кошице (Košice). Предусматривала развитие Чехословакии как народно-демократического государства двух равноправных народов — чехов и словаков, разрешение вопроса о Закарпатской Украине согласно волеизъявлению её населения, установление на местах власти избранных народом Национальных комитетов, предоставление трудящимся широких демократических свобод, предание суду лиц, сотрудничавших с оккупантами, запрещение фашистских и профашистских партий. К. п. намечала введение национального (государственного) управления имуществом немецких и венгерских собственников и коллаборационистов, наделение землёй безземельных и малоземельных крестьян. Основным принципом внешней политики К. п. выдвигала прочный союз и сотрудничество с СССР в военной, политической, экономической и культурной областях.