БСЭ БСЭ - Большая Советская Энциклопедия (КВ)

И ещё одна особенность аксиоматического подхода: проводимые в его рамках тщательные исследования позволяют обнаруживать те исходные положения в традиционной К. т. п., которые нуждаются в логическом и математическом уточнении.

Интенсивное развитие техники ускорителей заряженных частиц и обязанное ему небывалое увеличение потока экспериментальной информации об элементарных частицах заметно отразились на направлении теоретических поисков. Особое внимание привлекает величина, имеющая непосредственный физический смысл, — амплитуда рассеяния (квадрат её модуля определяет вероятность процесса). Для каждого процесса амплитуде рассеяния можно поставить в соответствие диаграмму, напоминающую по виду диаграмму Фейнмана, но имеющую принципиально иной смысл. Рассмотрим, например, диаграмму, изображенную на рис. 10 . Она похожа ( рис. 4и 5 ) на график вершинной части (и называется также вершинной), но теперь это не графическое изображение приближённого (полученного при помощи теории возмущений) решения некоторого уравнения, — график просто фиксирует процесс, в котором принимают участие частицы А , В и С . Если масса m A частицы А больше суммы масс m B + m C частиц В и С , то диаграмма описывает реальный распад А ® В + С . Если распад энергетически запрещен, то хотя бы одна из линий диаграммы относится к виртуальной частице. Кружок на рис. 10 означает, что вершина является физической, т. е. непосредственно соответствует тому, что выступает в эксперименте. Если линии А и В относятся к реальным нуклонам (например, протонам), а линия С изображает виртуальный фотон, то такая вершинная часть зависит лишь от одной переменной. Требования теории относительности заставляют выбрать в качестве такой переменной величину 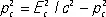, так как только такая комбинация из энергии E c и импульса р с частицы не меняется при переходе от одной инерциальной системы отсчёта к другой; величина р с называется четырёхмерным импульсом частицы С . Для реальной частицы 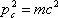, при этом говорят, что частица лежит на массовой поверхности. Виртуальные частицы лежат «вне массовой поверхности»; это обусловлено наличием заметного квантового разброса энергии, или, что эквивалентно, квантового разброса масс.

Зависимость амплитуды рассеяния от описывает наблюдаемое на опыте с распределение электрического заряда, магнитного момента и всех высших электрических и магнитных мультипольных моментов протона (так называемый электромагнитный форм-фактор протона). В рамках методов, о которых шла речь выше и которые типичны для квантовой электродинамики, такой форм-фактор в принципе следовало бы искать, анализируя «шубу» протона; как уже отмечалось, эффективных методов такого анализа не существует. Важная черта нового подхода — активное использование данных эксперимента для заполнения тех «брешей», которые возникают в теории.

Приведём ещё один важный пример «обобщённых» диаграмм — так называемую «четырёххвостку» ( рис. 11 ). Она изображает либо распад одной частицы на три ( А ® В + С + D ), если такой процесс энергетически разрешен, либо переходы типа «две частицы ® две частицы», в частности, если частицы в начале и в конце процесса одинаковы, — упругое рассеяние частиц. Рассмотрим этот последний процесс и, ради простоты, примем, что все частицы имеют одинаковую массу и нулевой спин. Тогда амплитуда рассеяния оказывается (если все 4 линии относятся к реальным частицам) зависящей лишь от двух инвариантных переменных. Обычно используются такие переменные: s = ( p A+ p B) 2— величина, равная квадрату энергии сталкивающихся частиц в системе центра инерции (т. е. в системе, в которой общий импульс частиц А и В равен нулю), и t = ( p A+ p C) 2 — величина, определяющая передачу импульса при рассеянии.

Приведённые на рис. 10и 11 диаграммы не исчерпывают, разумеется, всех возможностей. Однако они играют заметную роль и часто используются в качестве «узлов» при построении более сложных диаграмм, описывающих процессы с участием большего числа (более четырёх) частиц.

Для исследования амплитуды рассеяния f привлекается аппарат теории аналитических функций . При этом s и t , от которых зависит амплитуда рассеяния f ( s , t ), рассматривают как комплексные переменные. Такой подход оправдывается тем, что поведение аналитических функций в значительной мере определяется видом и положением так называемых особенностей функции (см. Особая точка ). Один из важнейших видов особенностей — полюс функции f ( z ) в некоторой точке z 0 отвечающий обращению функции f в этой точке в бесконечность типа 1/( z — z 0). Оказывается, что полюсы в амплитуде рассеяния могут получить наглядную интерпретацию. Если, например, в амплитуде рассеяния, описывающей процесс А + В ® С +D , появляется полюс вида 1/( s — m 2с 4 ), то это означает, что процесс идёт через промежуточную (виртуальную) частицу Q , А + В ® Q ® С + D , причём масса промежуточной частицы m Q = m . Полюс вида 1/( t — m 2с 4 ) соответствует диаграмме, изображенной на рис. 12 ; m есть масса промежуточной (виртуальной) частицы на этой диаграмме. Особенности др. типов также могут интерпретироваться физически как отражение неких важных процессов, проявляющихся на промежуточных этапах рассеяния. Если все эти особенности найдены, то на базе общих теорем теории аналитических функций можно пытаться полностью восстановить вид амплитуды рассеяния при всех значениях s и t , в частности при непосредственно интересующих физиков действительных значениях этих величин. Для нахождения особенностей используются как уже упоминавшиеся фундаментальные принципы релятивистской квантовой механики, так и ряд других. Важную роль играет условие унитарности; оно означает следующее: если процесс может происходить несколькими различными способами (протекать по различным «каналам»), например

A + B ® ,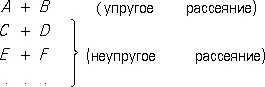

то полная вероятность всех возможных превращений равна единице. Несмотря на кажущуюся тривиальность, такие требования, как унитарность и положительность энергий физических частиц, вносят довольно жёсткие ограничения на амплитуды рассеяния.