БСЭ БСЭ - Большая Советская Энциклопедия (КР)

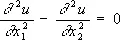(1)

имеет бесконечное множество решений u (x 1, х 2) = f (x 1+x 2) + f 1(x 1-x 2) , где f и f 1— произвольные дважды непрерывно дифференцируемые функции. Однако в прямоугольнике — а £ x 2 £ a, 0 £ x 1 £ l, плоскости с прямоугольными декартовыми координатами x 1, x 2 уравнение (1) имеет единственное решение u (x 1, x 2), удовлетворяющее краевым

u (0, x 2 ) = 0, u ( l , x 2 ) = 0, — а £ x 2 £ a, (2)

и начальным

u ( x 1, 0) = j( x 1 ) ,

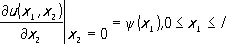(3)

условиям. При этом дважды непрерывно дифференцируемые функции j и y считаются наперёд заданными. Если переменное x 2 есть время t, то решение u ( х, t ) уравнения (1), удовлетворяющее условиям (2) и (3), описывает колебание упругой струны длины l с концами, закрепленными в точках (0, 0) и (0, l ). Изложенная задача нахождения решения уравнения (1) при условиях (2) и (3) — простейший пример так называемой смешанной задачи.

Вообще краевыми называют задачи, в которых в заданной области G пространства независимых переменных ( x 1,..., x n ) = х ищется решение u ( х ) = u ( x 1,..., x n ) уравнения

Du ( x ) = 0, x Î G (4)

при требовании, что искомая функция u ( х ) на границе S области G удовлетворяет краевому (граничному) условию

Bu ( у ) = 0, y Î S, (5)

где D и В — заданные операторы, причём, как правило, D — дифференциальный или интегро-дифференциальный оператор. Граница S называется носителем краевых данных (5).

Когда операторы D и В линейны, К. з. (4), (5) называется линейной. В предположениях, что S является ( n — 1 )-мерной гиперповерхностью, D — линейным дифференциальным оператором второго порядка

,

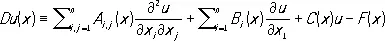а

,

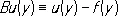где A i, j, B i, C, F, f — заданные функции, задача (4), (5) называется первой краевой задаей Дирихле. Если же

,

где a i , i = 1,..., n, f — заданные функции, то задача (4), (5) называется задачей наклонной (косой) производной. В частности, когда вектор ( a 1,..., a n ) совпадает с конормалью к S, задача наклонной производной носит название второй краевой задачи, или задачи Неймана. Задача Дирихле (Неймана) называется однородной, если

F ( x ) = 0, f ( y ) = 0 .

Задачи Дирихле и Неймана хорошо исследованы в ограниченных областях с достаточно гладкой границей в случае равномерной эллиптичности оператора D с действительными коэффициентами, т. е. при соблюдении условий

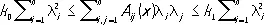, x Î G S (6)

где l 1,..., l n— произвольные действительные параметры, а k 0 и k 1 — фиксированные отличные от нуля числа одинакового знака.

При требовании достаточной гладкости коэффициентов операторов D и В и равномерной эллиптичности оператора D справедливы следующие утверждения: 1) число k линейно независимых решений однородной задачи Дирихле (Неймана) конечно; 2) для разрешимости задачи Дирихле (Неймана) необходимо и достаточно, чтобы функции F ( x ) и f ( y ) были подчинены дополнительным ограничениям типа условий ортогональности, число которых равно k ; 3) при соблюдении условия

С ( x ) £ 0, x Î G,

задача Дирихле всегда имеет и притом единственное решение; 4) в области G достаточно малого диаметра задача Дирихле всегда имеет и притом единственное решение и 5) при однозначной разрешимости задачи Дирихле (Неймана) малое изменение краевых данных вызывает малое изменение решения (т. е. решение устойчиво).

Когда D представляет собой оператор Лапласа 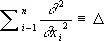, решение задачи Дирихле в ограниченной области с достаточно гладкой границей всегда существует и единственно, причём для некоторых областей частного вида оно выписывается в явном виде. Так, например, при n = 1 в интервале —1 < х < 1 это решение имеет вид

u ( х ) = ,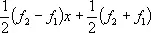

где f 1= u ( — 1), f 2= u (1), а при n = 2 и n = 3, соответственно, в круге | x | < 1 и шаре | x | < 1

,

,

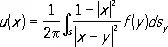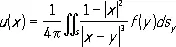где | х—у | — расстояние между точками х и у. Линейную К. з. называют фредгольмовой, если для неё имеют место сформулированные выше утверждения 1) — 5).

В К. з. для эллиптических уравнений обычно предполагается, что носителем краевого условия является вся граница S области G .

Если условие (6) равномерной эллиптичности не удовлетворено, но оператор D является эллиптическим в том смысле, что квадратичная форма 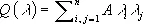в области D положительно (или отрицательно) определена, то иногда для сохранения фредгольмовости К. з. вполне определённую часть границы S области G следует освободить от краевых данных.

Линейная К. з. даже при требовании равномерной эллиптичности дифференциального оператора D, вообще говоря, не является фредгольмовой. В частности, задача наклонной производной может не оказаться фредгольмовой, если вектор ( a 1..., a n ) в некоторых точках границы S лежит в касательной к S плоскости.

Когда дифференциальный оператор D не является эллиптическим, К. з. (4), (5) может вовсе не иметь содержательного смысла, если часть границы S области G не освободить от краевых данных и на структуру носителя краевых данных не наложить определённые (порой весьма сильные) ограничения. Так, например, уравнение теплопроводности

,

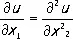являющееся типичным представителем уравнений параболического типа, в квадрате, ограниченном прямыми: x 1 = 0 , x 1= 1 , x 2= 0 , x 2= 1 , имеет единственное решение u ( x 1, x 2 ) , удовлетворяющее краевым условиям: