БСЭ БСЭ - Большая Советская Энциклопедия (МИ)

Лимбург. Миниатюра «Богатейшего часослова герцога Беррийского». Ок. 1411—16. Музей Конде. Шантийи. «Встреча трёх волхвов».

«Сердце и желание у волшебного источника». Миниатюра рукописи «Сердце, объятое любовью» (1457, Национальная библиотека, Вена).

Ж. Фуке. «Битва Иоафана и Симона Маккавея с бакхидами». Миниатюра «Иудейских древностей» Иосифа Флавия. 1470-е гг. Национальная библиотека. Париж.

«Ангел (символ евангелиста Матфея)». Миниатюра «Евангелия Хитрово» (конец 14 — начало 15 вв., Библиотека СССР им. В. И. Ленина, Москва).

Фрагмент египетского папирусного свитка «Книга мёртвых». 1400 до н. э.

Миниатю'рав литературе, театре, цирке, на эстраде, жанр «малых форм»: небольшое по размеру произведение — короткий рассказ, короткая пьеса, водевиль, интермедия, скетч, разговорная, хореографическая или музыкальная сценка, эстрадная или клоунская сцена и т. п. На М. строится репертуар специальных театров миниатюр.

Миниатю'р-полиго'н,учебный артиллерийский полигон, представляющий собой воспроизведение рельефа местности (рельефный план в масштабе обычно 1 : 300 — 1 : 1000), оборудованный целями (мишенями) и специальным устройством, имитирующим разрывы снарядов. Предназначен для обучения артиллерийской стрельбе по наземным и воздушным целям. М.-п. оборудуется в помещении или на открытой местности. Он позволяет практически изучать правила стрельбы артиллерии и проводить артиллерийские стрелковые тренировки.

Минима'ксв математике, значение

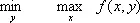
вещественной функции двух переменных f ( x, у ). С понятием М. связано понятие максимина, равного

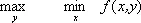
В теории антагонистических игр основным принципом оптимальности является принцип М., состоящий в стремлении игрока минимизировать свой выигрыш при наиболее неблагоприятном образе действий противника.

Минима'льная ло'гика,логическая система, являющаяся ослаблением интуиционистской логики и конструктивной логики за счёт исключения из числа постулатов формулы ùА É (А É В) (интерпретируемой как «из противоречия следует всё что угодно»). Несмотря на недоказуемость этого логического принципа и тем более формулы ù ù А É А («закона снятия двойного отрицания»), в минимальном исчислении высказываний (А. Н. Колмогоров, 1925, норвежский логик И. Иоганссон, 1936) можно доказать от противного отрицательные предложения, опираясь на «закон приведения к абсурду»: (А É В) É ((A É ù В) É ù А). Эту систему можно обычным образом расширить до минимального исчисления предикатов, играющего важную роль в работах по основаниям математики: его логические средства (хотя это явно и не оговаривается) используются, например, в доказательствах непротиворечивости классической арифметики, предложенных немецкими логиками Г. Генценом (1936, 1938) и К. Шютте (1951) и П. С. Новиковым (1943) (см. Метаматематика ) . Это исчисление используется также как логическая база метатеории в работах по ультраинтуиционистскому обоснованию математики (см. Аксиоматическая теория множеств, Аксиоматический метод ) . Ослабление (сужение) М. л. посредством исключения из числа аксиом «закона приведения к абсурду» приводит к положительной логике.

Лит.: Колмогоров А. Н., О принципе tertium non datur, «Математический сборник», 1925, т. 32, в. 4, с. 646—67; Клини С. К., Введение в метаматематику, пер. с англ., М., 1957, с. 94, 490—91; Johansson J., Der Minimalkalkül, ein reduzierter Formalismus, «Compositio mathematica», 1937, v, 4, fasc. 1; Wajsberg M., Untersuchungen über den Aussagenkalkül von A. Heyting, «Wiadomosci Mathematyczne», 1939, t. 46.

Ю. А. Гастев.

Минимальные поверхности,поверхности, у которых средняя кривизна во всех точках равна нулю (см. Кривизна ) . М. п. появляются при решении следующей вариационной задачи: в пространстве дана некоторая замкнутая кривая; среди всех возможных поверхностей, проходящих через эту кривую, найти такую, для которой часть её, заключённая внутри кривой, имела бы наименьшую площадь (минимальную площадь — отсюда название). Если заданная кривая — плоская, то решением, очевидно, будет ограниченный этой кривой кусок плоскости. В случае неплоской кривой необходимое условие, которому должна удовлетворять поверхность с минимальной площадью, было установлено Ж. Лагранжем в 1760 и несколько позже истолковано геометрически Ж. Мёнье в форме, эквивалентной требованию, чтобы средняя кривизна обращалась в нуль. Хотя это условие не является достаточным, т. е. не гарантирует минимума площади, однако впоследствии название «М. п.» было сохранено за всякой поверхностью с нулевой средней кривизной. Если предположить поверхность заданной уравнением z = f ( х , у ), то, приравнивая нулю выражение для средней кривизны, приходят к дифференциальному уравнению с частными производными 2-го порядка:

(1 + q 2) r - 2 pqs + (1 + p 2) t = 0,

где

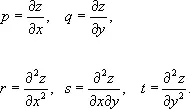
Исследованием этого уравнения в различных формах занимались многие математики, начиная с Ж. Лагранжа и Г. Монжа. Примерами М. п. могут служить: обыкновенная винтовая поверхность; катеноид— единственная (вещественная) М. п. среди поверхностей вращения; «поверхность Шерка», определяемая уравнением

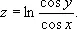
М. п. имеет во всех точках неположительную полную кривизну. Бельгийский физик Ж. Плато предложил способ экспериментального осуществления М. п. при помощи мыльных плёнок, натянутых на проволочный каркас.

Лит.: Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1, М. — Л., 1947; Курант Р., Роббинс Г., Что такое математика, пер. с англ., 2 изд., М., 1967; Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957.