БСЭ БСЭ - Большая Советская Энциклопедия (МИ)

Лит.: Цанева М., С. Минков, С., 1961; Султанов С., Насаме със С. Минков, С., 1972.

В. И. Злыднев.

Минко'вский(Minkowski) Герман (22.6.1864, Алексоты Минской губернии, — 12.1.1909, Гёттинген), немецкий математик и физик. Профессор университетов в Бонне (с 1893), Кенигсберге (с 1894), Цюрихе (с 1896), Гёттингене (с 1902). М. разработал т. н. геометрию чисел, в которой употребляются геометрические методы решения трудных вопросов теории чисел. Геометрию чисел одновременно с М. и независимо от него разрабатывал Г. Ф. Вороной. Работы их дополняют друг друга. От геометрии чисел М. перешёл к работам по теории многогранников и геометрии выпуклых тел, где им были получены важные общие результаты. М. — автор работ по математической физике, гидродинамике и теории капиллярности, теории относительности. В 1907—08 дал геометрическую интерпретацию кинематики специальной теории относительности, введя т. н. Минковского пространство.

Соч.: Geometrie der Zahlen, Lfg 1—2, Lpz., 1896—1910; Gesammelte Abhandlungen, hrsg. von D. Hilbert, Bd 1—2, Lpz. — B., 1911.

Лит.: Делоне Б. Н., Герман Минковский, «Успехи математических наук», 1936, в. 2.

Минко'вского нера'венство,неравенство вида

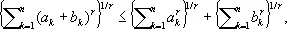
где a k и b k ( k = 1, 2,..., n ) — неотрицательные числа и r > 1. М. н. имеет аналоги для бесконечных рядов и интегралов; оно было установлено Г. Минковским в 1896 и выражает тот факт, что в n -мерном пространстве, для которого расстояние между точками x = ( x 1, x 2, ..., x n ) и y = ( y 1, y 2, ..., y n ) имеет величину

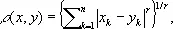
сумма длин двух сторон треугольника больше длины третьей стороны.

Минко'вского простра'нство,четырёхмерное пространство, объединяющее физическое трёхмерное пространство и время; введено Г. Минковским в 1907—1908. Точки в М. п. соответствуют «событиям» специальной теории относительности (см. Относительности теория ) .

Положение события в М. п. задаётся четырьмя координатами — тремя пространственными и одной временной. Обычно используются координаты x 1 = х, x 2 = у, х 3 = z , где х, у, z — прямоугольные декартовы координаты события в некоторой инерциальной системе отсчёта, и координата x 0 = ct , где t — время события, с — скорость света. Вместо xo можно ввести мнимую временную координату x 4 = ix 0 = ict.

Из специальной теории относительности следует, что пространство и время не независимы: при переходе от одной инерциальной системы отсчёта к другой пространственные координаты и время преобразуются друг через друга посредством Лоренца преобразований. Введение М. п. позволяет представить преобразования Лоренца как преобразование координат события x 1, x 2, x 3, x 4 при поворотах четырёхмерной системы координат в этом пространстве.

Основной инвариант М. п. — квадрат длины четырёхмерного вектора, соединяющего две точки — события, не меняющийся при вращениях в М. п. и равный по величине (но противоположный по знаку) квадрату четырёхмерного интервала ( s 2 AB ) специальной теории относительности:

(x 1A— x 1B) 2 + (х 2А— x 2B) 2 + (x 3A— x 3B) 2+ (x 4A— x 4B) 2= (x A — x B) 2 + (у А— y B) 2+ (z A— z B) 2 — c 2 (t A— t B) 2= -s 2 AB

(индексами А и В отмечены пространственные координаты и время событий А и В соответственно). Своеобразие геометрии М. п. определяется тем, что это выражение содержит квадраты составляющих четырёхмерного вектора на временную и пространственные оси с разными знаками (такая геометрия называется псевдоевклидовой, в отличие от евклидовой геометрии, в которой квадрат расстояния между точками определяется суммой квадратов составляющих вектора, соединяющего точки, на соответствующие оси). Вследствие этого четырёхмерный вектор с отличными от нуля составляющими может иметь нулевую длину; это имеет место для вектора, соединяющего два события, связанных световым сигналом:

(x A— x B) 2 + (у А— у В) 2 + (z A— z B) 2 = c 2 (t A— t B) 2 .

Геометрия М. п. позволяет наглядно интерпретировать кинематические эффекты специальной теории относительности (изменение длин и скорости течения времени при переходе от одной инерциальной системы отсчёта к другой и т. д.) и лежит в основе современного математического аппарата теории относительности.

Г. А. Зисман.

Ми'нкус(Minkus) Людвиг Федорович (настоящее имя — Алоизий Людвиг) (23.3.1826, Вена, — 1907, там же), скрипач и композитор. По национальности чех (по другим сведениям — поляк). С начала 50-х до конца 80-х гг. жил в России. В 1853—55 капельмейстер крепостного оркестра Н. Б. Юсупова в Петербурге, в 1861—72 солист оркестра Большого театра в Москве. В 1866—72 преподавал в Московской консерватории. В 1872—86 работал композитором балетной музыки при Театральной дирекции в Петербурге. После 1890 жил в Вене. Первый успех — совместная работа с Л. Делибом балет «Ручей» (1866). В 1869 в Москве в Большом театре был поставлен балет «Дон Кихот» (автор сценария и балетмейстер М. И. Петипа), сохраняющийся в репертуаре современных театров. В последующие годы продолжалось творческое содружество Петипа и М. (М. написал для него 16 балетов). Музыка М. мелодична, отличается чётким танцевальным ритмом. Среди других балетов М.: «Пахита» (1846, совместно с Э. Дельдевезом), «Фиаметта, или Торжество любви» (1864), «Баядерка» (1877), «Дочь снегов» (1879). М. принадлежат также произведения для скрипки.

Лит.: Красовская В., Русский балетный театр второй половины XIX века, Л. — М., 1963.

Ми'нкусМихаил Адольфович [12 (25).12.1905, Одесса, — 31.8.1963, Турку, Финляндия], советский архитектор. В 1930 окончил ленинградскую АХ, где учился у И. А. Фомина и В. А. Щуко. Много работал совместно с В. Г. Гельфрейхом (в т. ч. высотное здание министерства иностранных дел на Смоленской площади в Москве, 1948—1952; Государственная премия СССР, 1949), И. А. Фоминым, В. А. Щуко. Другие работы: многоэтажный гараж на Краснопресненском валу (1936—41, с соавторами) и жилые дома на Смоленской площади и набережной (1956—63, с соавторами) — в Москве; здание торгпредства СССР в Дели в Индии (1956—59, совместно с архитектором Н. С. Полюдовым), планировка и застройка микрорайона Давыдково в Москве (с 1963, с соавторами). Автор ряда надгробий и архитектурной части памятников.