БСЭ БСЭ - Большая Советская Энциклопедия (МН)

Лит. см. при ст. Многогранник.

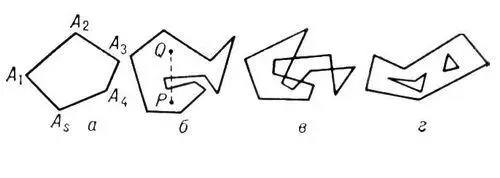
Рис. 1 к ст. Многоугольник.

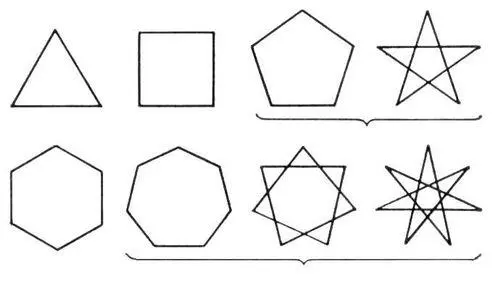
Рис. 2 к ст. Многоугольник.

Многоуго'льник сил,ломаная линия, которая строится для определения главного вектора (геометрической суммы) данной системы сил. Чтобы построить М. с. для системы сил F 1 , F 2 , ..., F n( рис. , а), надо от произвольной точки а поочерёдно отложить в выбранном масштабе вектор 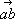, изображающий силу F 1, от его конца отложить вектор 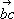, изображающий силу F 2, и т. д. и от конца m предпоследней силы отложить вектор 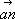, изображающий силу F n( рис. , б). Фигура abc ... mn и называется М. с. Вектор an , соединяющий в М. с. начало первой силы с концом последней, изображает геометрическую сумму R данной системы сил. Когда точка n совпадает с а , М. с. называется замкнутым; в этом случае R = 0. Правило М. с. может быть получено последовательным применением правила параллелограмма сил.

Построением М. с. пользуются при графическом решении задач статики для систем сил, расположенных в одной плоскости.

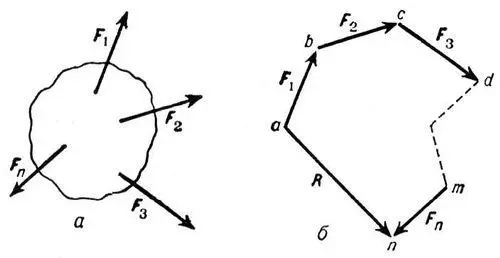
Рис. к ст. Многоугольник сил.

Многоу'стки,класс червей; то же, что моногенетические сосальщики.

Многофото'нные проце'ссы,процессы взаимодействия электромагнитного излучения с веществом, сопровождающиеся поглощением или испусканием (или тем и другим) нескольких электромагнитных квантов ( фотонов ) в элементарном акте.

Основная трудность наблюдения М. п. — их чрезвычайно малая вероятность по сравнению с однофотонными процессами. В оптическом диапазоне до появления лазеров наблюдались только двухфотонные процессы при рассеянии света: резонансная флуоресценция (см. Люминесценция ) , релеевское рассеяние света, Мандельштама — Бриллюэна рассеяние и комбинационное рассеяние света. При резонансной флуоресценции ( рис. , а) атом или молекула поглощают в элементарном акте одновременно один фотон возбуждающего излучения ћ w 1и испускают один фотон ћ w 2той же самой энергии. Рассеивающий атом при этом снова оказывается на том же самом уровне энергии E 1. В элементарном акте бриллюэновского и комбинационного рассеяний в результате поглощения и испускания фотонов рассеивающая частица оказывается на уровне энергии, удовлетворяющем закону сохранения энергии для всего двухфотонного процесса в целом: увеличение энергии частицы E 2— E 1равно разности энергий поглощённого и испущенного фотонов ћ w 1— ћ w 2( рис. , б). После появления лазеров стало возможным наблюдение процессов многофотонного возбуждения, когда в элементарном акте одновременно поглощается несколько фотонов возбуждающего излучения ( рис. , в). Так, при двухфотонном возбуждении атом или молекула одновременно поглощают два фотона ћ w 1и ћ w 2и оказываются в возбуждённом состоянии с энергией E 2= E 1+ ( ћ w 1+ ћ w 2) (см. Вынужденное рассеяние света, Нелинейная оптика ) .

Представление о М. п. возникло в квантовой теории поля для описания взаимодействия излучения с веществом. Это взаимодействие описывается через элементарные однофотонные акты поглощения и испускания фотонов, причём р -приближению теории возмущений соответствует элементарный акт с одновременным участием р фотонов; р -фотонный переход можно рассматривать как переход, происходящий в р этапов через р — 1 промежуточных состояний системы: сначала поглощается (или испускается) один фотон и система из состояния E 0переходит в состояние E 1, затем поглощается (или испускается) второй фотон и система оказывается в состоянии E 2и т. д.; наконец, в результате р элементарных однофотонных актов система оказывается в конечном состоянии E р.

В случае М. п. с поглощением или вынужденным испусканием р фотонов одинаковой частоты w величина вероятности перехода пропорциональна числу фотонов этой частоты в степени р , т. е. интенсивности излучения в этой степени.

Вероятность М. п. с участием р фотонов отличается от вероятности М. п. с участием ( р — 1) фотона множителем, который в оптическом диапазоне для нерезонансных разрешенных дипольных электрических переходов (см. Квантовые переходы ) ~ ( Е св /Е ат) 2, где Е св— амплитуда напряжённости электрического поля излучения, Е ат— средняя напряжённость внутриатомного электрического поля (~ 10 9 в/см ) . Для всех нелазерных источников излучения Е св<< Е ати с увеличением числа фотонов вероятность перехода резко уменьшается. В случае лазерных источников уже достигнуты столь большие плотности мощности излучения (10 15 вт/см 2) , что Е св /Е ат~ 1 и вероятности М. п. с участием большого числа фотонов становятся сравнимыми с вероятностями однофотонных переходов.

Правила отбора для М. п. отличны от правил отбора для однофотонных. В системах с центром симметрии дипольные электрические переходы с участием чётного числа фотонов разрешены только между состояниями с одинаковой чётностью, а с участием нечётного числа фотонов — между состояниями с разной чётностью. На новых правилах отбора для М. п. основано одно из наиболее принципиальных применений М. п. — многофотонная спектроскопия. Измерение спектров многофотонного поглощения позволяет оптическими методами исследовать энергетические состояния, возбуждение которых запрещено из основного состояния в однофотонных процессах.

В отличие от однофотонных процессов, закон сохранения энергии при М. п. может быть выполнен при результирующем переходе атома из более низкого в более высокое энергетическое состояние не только с поглощением, но и с испусканием отдельных фотонов. Поэтому М. п. лежат в основе методов преобразования частоты излучения лазеров и создания новых перестраиваемых по частоте лазерных источников излучения (генераторов гармоник, генераторов комбинационных частот, параметрических генераторов света и т. п.). На основе М. п. возможно также создание перестраиваемых по частоте источников мощного оптического излучения.